CF1379C Choosing flowers

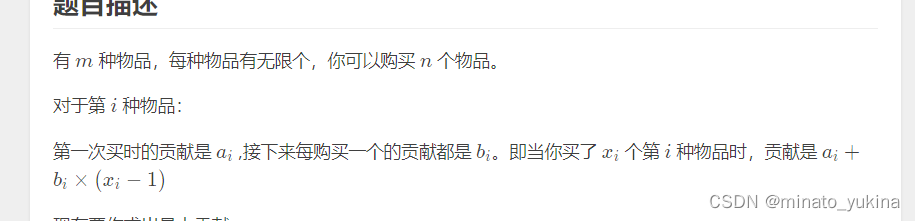
试着找出一个比较靠谱的思路先,重点在于物品买完第一次后会变化价格,之后都不会再变了,贪心地,如果我们重复地购买了一件物品,那么很显然我们只会重复购买一件物品多次,但这个物品可能不是 m a x ( b i ) max(b_i) max(bi​). 我们考虑枚举每个物品作为这个购买了多次 b i b_i bi​.显然,如果我们认为当前这个物品购买了多次 b i b_i bi​,一定不会购买其他物品的 b i b_i bi​,而只会购买他们的 a i a_i ai​.那么把 a i a_i ai​降序排序,利用二分搜索找到一个 p o s pos pos,使得 a p o s > b i a_{pos}>b_i apos​>bi​. 求得这个前缀和,也就是我们要购买 a 1 到 a p o s 所有的 a a_1到a_{pos}所有的a a1​到apos​所有的a,余下的 n − p o s 全部用来购买物品 i n-pos全部用来购买物品i n−pos全部用来购买物品i.

/*+
You held me down but I broke free,
I found the love inside of me.
Now I don't need a hero to survive
Cause I already saved my life.
*/
#include
using namespace std;
const int maxn = 1e6+5;
const int INF = 1e9+7;
typedef long long ll;
typedef pair pii;
#define all(a) (a).begin(), (a).end()
#define pb(a) push_back(a)
vector G[maxn];
struct Node{
	int a,b;
	bool operator rhs.a;
	}
}t[maxn];
int n,m;
ll pre[maxn];
int find(int k){
	//lower_bound to find a_pos > b[k]
	int ans = 0,L = 1,R = m;
	while(Lt[k].b) ans = mid,L = mid+1;
		else R = mid-1;
	}
	return ans;
}
int main(){
    ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int T;cin>>T;
	while(T--){
		cin>>n>>m;
		for(int i=1;i>t[i].a>>t[i].b;
		}
		sort(t+1,t+1+m);
		for(int i=1;i=i) sum+= 1LL*res*t[i].b;
				else sum+= t[i].a + 1LL*(res-1)*t[i].b;
			}
			ans = max(sum,ans); 
		}
		cout