1. Introduction-Machine Learning for Graphs

目录

一、Machine Learning with Graphs

（一）Why Graphs？

（二）Graphs：Machine Learning 

（三）Course Outline

二、Applications of Graph ML

（一）Node-level ML Tasks

例：蛋白质的三维构成

（二）Edge-level ML Tasks

例1：推荐系统（Recommender Systems）

例2：药物组合的副作用预测

（三）Subgraph-level ML Tasks

例：交通预测（旅程时间预测）

（四）Graph-level ML Tasks

例1：药物发现

例2：基于物理的模拟

三、Choice of Graph Representation（图表征）

（一）Graph & Graph Representation

（二）Some Concepts

（三）Representing Graphs

（四）Connectivity

 四、Summary

一、Machine Learning with Graphs

图（graph）— structured data

How apply novel machine learning methods to it？

（一）Why Graphs？

1、图（Graph）是描述和分析具有关系和交互的实体的通用语言。

• 不能把世界或某个给定领域看作是一组孤立的数据点
• 应从这些实体之间的网络和关系来考虑，即这些实体之间有一个基本的关系图，根据这些关系图的结构，这些实体彼此关联

2、有很多类型的数据可以用图（Graphs）表示，并对这些图形关系进行建模。

以下所有这些域本质上都是网络（Networks）或图（Graphs），这种表示方式能让我们捕捉不同领域中不同对象或实体间的关系。

• Event Graphs   基础设施或事件
• Computer Networks   计算机网络
• Disease Pathways   疾病路径
• Food Webs   食物网中的生物体
• Particle Networks   粒子网络（物理）
• Underground Networks
• ---------------------------------------------------------------------------------------------------------------------------
• Social Networks   社交网络
• Economic Networks   经济网络
• Communication Networks   通信网络
• Citation Networks   不同论文之间的引用网络
• Internet   互联网（作为一个巨大的通信网络）
• Networks of Neurons   大脑中的神经元连接网络
• ---------------------------------------------------------------------------------------------------------------------------
• Knowledge Graphs   可以把知识和事实表示为不同实体之间的关系
• Regulatory Networks   将自身的调节机制描述为由不同实体之间的连接所控制的过程
• Scene Graphs   把现实世界的场景作为场景中物体之间关系的图来表示
• Code Graphs   可以使用计算机编码软件并将其表示为不同函数之间调用的图或代码的结构，由抽象语法树捕获
• Molecules   把分子表示为由节点nodes（原子atoms）和边edges（键bonds）组成的一组图
• 3D Shapes   在计算机图形学中，可以用三维图形来表示

3、网络（Networks）&  图（Graphs）的类型  

• Networks（Natural Graphs）：其基础领域可以自然地表示为图 社交网络：社会是70亿人的集合及他们之间的联系 通讯/交易：电子设备间的通讯、电话、金融交易等等 生物医学：基因、蛋白质调节生物过程、不同生物实体之间的相互作用 大脑神经元间的连接
• Graphs（as a representation） 信息和知识：经常被组织和连接 软件：可以用图表示 相似网络图：多次取数据点，连接相似的数据点，这将创建一个相似网络图 具有自然关系结构的领域：分子、场景图、三维形状、基于粒子的模拟（物理学，模拟粒子间是如何相互联系的）

如何利用这种关系结构来做出更好、更准确的预测？

复杂的域有丰富的关系结构，可以用图表示。通过明确地为这些关系建模，我们将能够实现更好的性能，建立更准确的模型，做出更准确的预测。

（二）Graphs：Machine Learning 

1、现代深度学习工具箱专用于简单数据类型：

• sequence（序列）：具有线性结构，如文本 text 或 语音 speech
• grid（网格）：可以调整大小并具有空间局部性，故可以表示为固定大小标准，如 image

2、为什么 Graph Deep Learning 困难？

Graphs 和 Networks 更加复杂

• 具有任意大小和复杂的拓扑结构
• 无网格或序列中的空间局部性
• 通常是动态的，具有多模式的特征

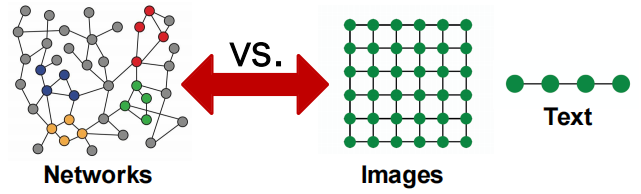
 从图中可以看出：

• 网络（Networks）无参照点，无空间局部性的概念，无固定的节点顺序可以进行深度学习
• 图像（Images）只有上下左右四个方向，文本（Text）只有左右两个方向。

3、如何开发适用范围更广的神经网络（Natural Networks）以适用于复杂的数据类型，如图（Graphs）？

  关系数据图（Graphs）是深度学习和表示学习研究的新前沿

（1）Deep Learning in Graphs

建立神经网络：

• Input：Graph
• output：Prediction（可以是以下3种级别的预测：individual nodes；pairs of nodes or links；a brand new generated graph）

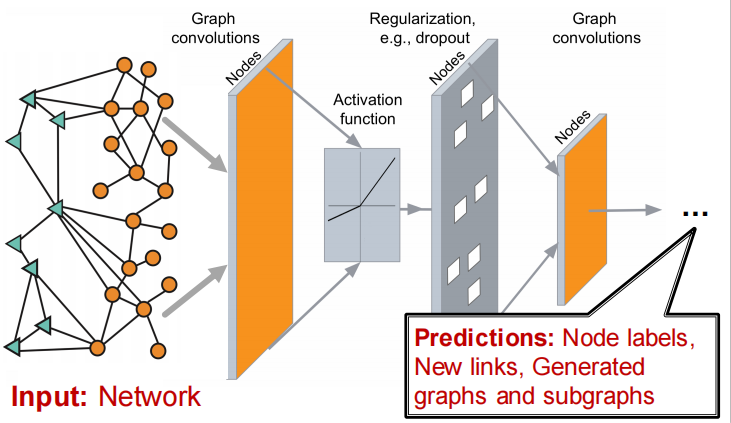
 （2）Representation Learning

不进行特征工程，自动提取或学习图中的特征

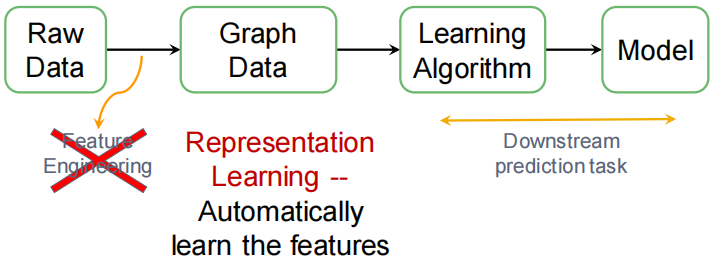
 将图的节点映射到d维向量或embedding

goal：学习函数f，它会把节点映射到d维实值向量上，这个向量将调用的是一个表示（representation — an embedding of a given node/link/an entire graph）

（三）Course Outline

Part I：

• Machine Learning和图的传统方法：Graphlets，Graph Kernels
• 生成泛型节点嵌入（node embeddings）的方法：DeepWalk，Node2Vec
• 图神经网络（Graph Neural Networks，GNN）架构：GCN（Graph Convolutional Neural Network）图卷积神经网络GraphSAGEGAT（Graph Attention Network）
• GNN的表达能力、背后理论、如何把它们放大到非常大的图

Part II：

• 异质图（Heterogeneous Graphs，HG）
• 知识图（Knowledge Graphs，KG）及其在逻辑推理（logical reasoning）中的应用，方法：TransE、BetaE
• 如何为图建立深层生成模型（Deep Generative Models）：GraphRNN
• 讨论在生物医学（Biomedicine）上的应用、各种科学（Science）应用、以及在行业（Industry）中的应用，如推荐系统、欺诈检测

重点：

1. 图神经网络（Graph Neural Networks，GNN）
2. 图的表示学习（Representation Learning in Graphs）

二、Applications of Graph ML

图机器学习研究的应用（涉及许多不同的应用）及其影响

不同类型的任务：

• individual nodes（单个节点）： 节点分类，预测节点的属性 例：对在线用户/项目进行分类
• edges（pairs of nodes）： 预测是否一对节点间缺少连接 例：知识图谱补全
• subgraphs of nodes：聚类/群体检测，来区分紧密联系的图的子部分 例：社交圈检测
• the entire graphs： 分为2种：（1）a graph level prediction：          图分类          例：将分子表示为图，预测分子的特性（药物设计）（2）graph generation  图生成（例：药物发现以产生新的分子结构）          graph evolution  图演化（例：对各种物理现象进行精确模拟，这些现象可以用图表示）

通过这些不同级别的任务，展示不同领域中的不同应用。

（一）Node-level ML Tasks

对于图中的每个节点，预测它在空间中的位置

例：蛋白质的三维构成

1、背景

• 蛋白质可以调节各种生物进程，由氨基酸构成，可以看成一个氨基酸序列。由于磁力和不同种类的力，这些蛋白质不是以链或株的形式存在，事实上它们折叠成一种极其复杂的形状。
• 药物作用是绑定或改变不同蛋白质的行为，进而改变身体的生物进程。
• 生物学中非常重要且尚未解决的问题之一是：若给你一个氨基酸序列，预测隐含之下的蛋白质的3D结构。即：仅仅凭借氨基酸序列，通过计算预测蛋白质的3D结构。

2、突破

• 让潜在的蛋白质以图的形式呈现：“Spatial graph”  空间图  Nodes：蛋白质序列中的氨基酸  Edges：空间上彼此接近的氨基酸
• 图表征和图神经网络技术的使用：给定全部氨基酸位置，以及它们之间的邻近边界，GNN路径经过训练可以预测氨基酸的新位置，用这种方法蛋白质的折叠能够被模拟，并且分子的最终位置也可以被预测到

3、成果

AlphaFold：蛋白质折叠应用程式

（二）Edge-level ML Tasks

link prediction / 不同节点（pairs of nodes）之间的关系

例1：推荐系统（Recommender Systems）

1、用户与项目（产品、电影、歌曲等）交互

• Nodes：Users 和 Items
• Edges：User-Item 的交互

2、Goal：若一个用户消费、购买、评论了一个指定的项目，或听了一首指定的歌曲、看了一部指定的电影，基于构建的图的结构以及用户和项目的属性，我们能预测或推荐给用户他们在以后可能会感兴趣的其他项目

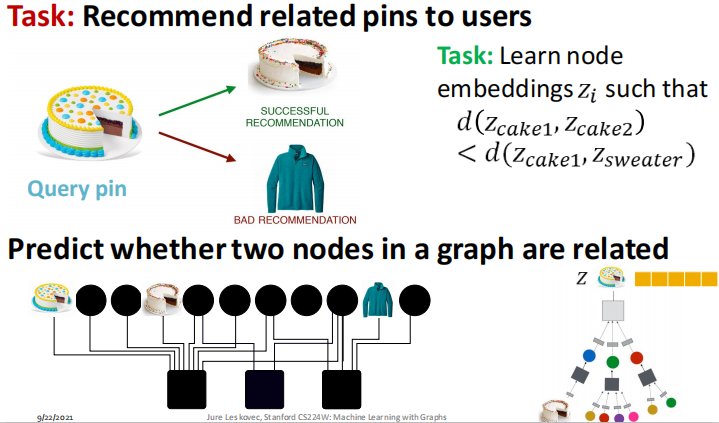
3、PinSage：基于图的推荐（基于图表征学习和 GNN 进行预测）

Ying et al., Graph Convolutional Neural Networks for Web-Scale Recommender Systems, KDD 2018   https://arxiv.org/pdf/1806.01973.pdf 是一个全网级别的大型推荐系统，使用random walk和图卷积神经网络，结合图结构和节点特征来产生节点嵌入

相关联的节点应该更紧密地嵌在一起，它们之间的距离相对于那些彼此没有关联的节点对要更近

步骤：

• 创建二分网络（bipartite graph，二部图），把图像（images）放在上面，用户（users）放在底部
• 定义一个神经网络方法，带有这些不同标识的特征信息或属性信息，即大体上图像的内容，并跨越潜在图将这个神经网络方法加以转换，以此得出给定图像的可靠嵌入

images+graph structure 比仅仅考虑 images 形成的推荐系统要有效的多

例2：药物组合的副作用预测

1、背景

• 很多病人同时服用多种药物，来治疗复杂或并存的疾病。这些药物彼此之间会相互作用，导致新的不良副作用，基本上，药物之间的相互作用会导致额外的疾病
• 不同药物的组合数量过于庞大，所以无法在实验或临床试验中测试每种药物的组合以看它会导致什么样的副作用

2、目标

• 建立预测引擎来处理任何一种药物组合，以此来预测这些药物将如何相互作用，或它们会产生何种副作用
• 图问题 △：不同药物 ○：体内蛋白质 药物的工作方式是针对不同蛋白质起作用，故这部分是△和○之间的边来表示 两层异构网络
• 在蛋白质互相作用网络中，进行试验测试两种蛋白质是否会自然地相聚并相互作用，以调节特定的生物过程或功能。通过试验可知哪些蛋白质会相互作用（○与○之间的边）
• r1 和 r2 代表已知副作用。显然副作用网络是不完整的，故要预测缺失边与联系，即预测若一个人同时服用两种药物，预计会产生什么样的副作用。问题变为：图中△节点之间的链路预测 （三）Subgraph-level ML Tasks

子图级别的机器学习任务

例：交通预测（旅程时间预测）

1、Road Network as a Graph

• Nodes：路段
• Edges：路段之间的连通性
• Prediction：到达时间（ETA）

2、图神经网络

• 基于每条路段的路况与交通模式，以及旅程出发地与目的地之间的路径而训练
• 训练 GNN 方法来预测估计到达时间 / 旅途时间 （四）Graph-level ML Tasks

例1：药物发现

基于图的机器学习用来发现新药、新抗生素（小分子图）

问题：哪些分子具有治疗效果？（哪些分子应被优先考虑？）

1、每个分子都可以表示为一个图

• 节点：原子
• 边：化学键

2、用GNN对不同分子进行分类，并从大量、数十亿的候选分子中预测可能有治疗效果的分子。之后，这些预测会在实验室被进一步验证

3、图生成（Graph generation）：一种发现新分子的方式，帮助生成新结构及目标方向的各种新分子，而新分子是之前从未被合成或考虑到的

分子生成/优化：拥有具有特定治疗效果的分子的一小部分构成，想要完善剩下的分子构成，这样一来可以提升分子的一个特定属性

• Use case 1：生成具有高度药物相似性的新分子
• Use case 2：对现有分子进行优化，进而使得分子具有理想的特性

例2：基于物理的模拟

1、Physical Simulation as a graph

• Nodes：用一组粒子来代表材料
• Edges：粒子组能捕捉的粒子之间的相互作用
• Task：预测此图在未来将如何演变（即，预测这种材料将如何变形）

2、步骤（迭代过程）

• 取材料，以一组粒子代表它。根据距离及粒子间的相互作用，生成邻近图
• 将图机器学习加之运用，这是一个GNN，有着当前属性：粒子位置、粒子速率，以此来推断未来粒子的位置和速率
• 基于这个预测，可以将粒子移动或演进到它们的新位置
• 回到第一步，基于这个新的邻近图，预测新的粒子位置，移动粒子 三、Choice of Graph Representation（图表征）

（一）Graph & Graph Representation

1、Network 的组成部分

图（G）是由一组节点（N）和一组边（E）组成的

• Objects：nodes（节点）、vertices（顶点）      N 
• Interactions：links、edges               E
• Systems：network、graph       G（N，E）

2、图是一种通用的语言

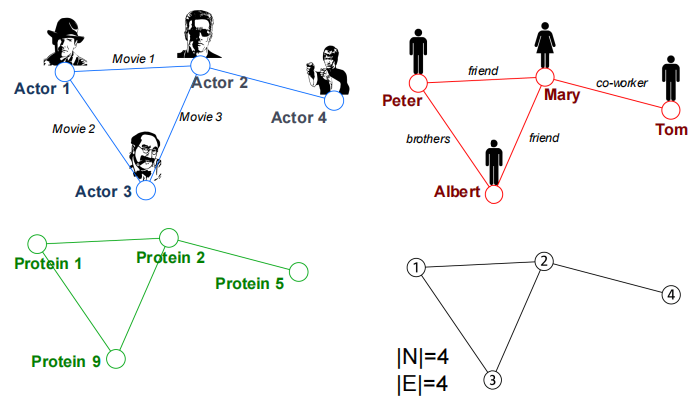
• 图1：根据 actor 出演的 movie 将他们联系在一起
• 图2：根据 people 之间的 relationship 将他们联系在一起
• 图3：根据蛋白质分子之间的相互作用将它们联系在一起

3个例子都会得到相同的基本数学表达式（图4），这意味着：不管节点对应的是 actor、people、蛋白质等的分子，相同的机器学习算法都可以做出预测。

 3、选择一个合适的表征

• 节点（nodes）和连接（links）的选择非常重要
• 如果选择不当，潜在的网络质量及图表征质量可能就会很低下
• 选择适当的图对给定领域或给定问题进行表征，将会决定能否成功使用网络 （二）Some Concepts

1、无向图（Undirected）VS  有向图（Directed）

• 无向图：对称、互惠关系（合作、友谊、蛋白质分子间的相互作用）
• 有向图：如电话来电、金融交易、微博上的关注

2、节点度（Node Degrees）

• 无向图：给定节点的邻近边数量
• 有向图：入度（指向节点的边数） &  出度（从节点向外指的边数）

平均节点度：网络中所有节点度的平均值，为网络中的边数（E）除以节点数（N）的两倍，即：

• 当我们计算节点度时，每条边都计算2次（每条边的端点计算1次，因为每条边有2个端点，故而）
• 若有1个自循环，会给节点增加2个节点度（因为每个端点连接同一个节点）

 3、二部图（Bipartite Graph）

（1）定义：包含2种不同类型节点的图，图中的节点仅与其他类型的节点相互联系，而非同一类之间的联系。例：

• Authors-to-Papers（they authored）
• Actors-to-Movies（they appeared in）
• Users-to-Movies（they rated）
• Recipes-to-Ingredients（they contain）
• Customers-to-Products（they bought）

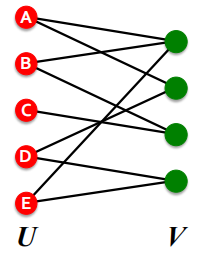图中的节点可以分为2个分区，且边只从左边的分区往右边连接，而非在同一分区里连接

（2）折叠/投射网络（Folded/Projected Networks）

例如：作者合作网络、电影联合评级网络

连接节点的方式是：将在一对节点间创建连接，如果它们至少有一个共同的邻近节点

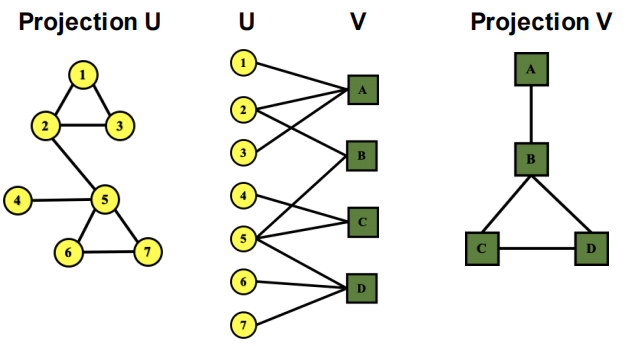若U表示作者，V表示论文，则中间的图表示一个合作/共同作者关系图

4、More Types of Graphs

（1）Unweighted  VS  Weighted

 右图中，邻接矩阵不是用二进制（0/1）表示，而是用边的属性（权重）表示的，让邻接矩阵获得真实值。例如，从右图矩阵中可以看出，节点 2 和节点 4 间的联系更强（因为权重为4）

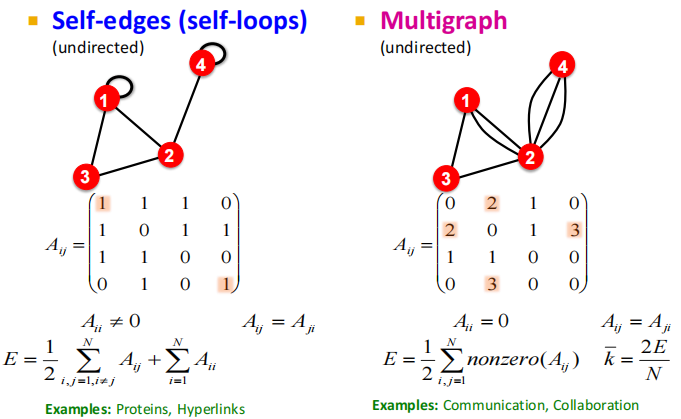
（2）Self-edges（self-loops） VS  Multigraph

• 左图：考虑具有自循环的节点，如节点4的度数是3（1个自循环增加2个节点度）。自循环对应于邻接矩阵对角线上的输入项
• 右图：多边图，即一对节点之间有多条边。有时可将多边图视为一个加权图，图中矩阵的输入项代表边的数量。但有时想单独表示每条边，因为这些边可能具有不同的属性。例：电话交易（一对节点间可以有多个交易）

（三）Representing Graphs

1、邻接矩阵（Adjacency Matrix）：若节点 i 和节点 j 连接（没连接），矩阵 Aij 的输入将被设置为 1（0）

• 无向图：邻接矩阵是对称的，节点度数为给定行/列的总和
• 有向图：邻接矩阵不对称，入（出）度为图的邻接矩阵的列（行）的总和

邻接矩阵是稀疏（Sparse）的：

• 一个基于n个节点的网络，其中一个节点的最大度数（节点的连接数）为 n-1
• 而现实世界的网络中 k