最大化偏差问题与Double Q-Learning(一)——最大化偏差问题介绍

目录

本系列将介绍求解时序差分控制过程中算法出现的最大化偏差问题以及解决方法——Double Q learning算法。

什么是最大化偏差

前面分别介绍了基于同轨策略求解时序差分控制(SARSA)和基于离轨策略求解时序差分控制(Q-Learning)，我们发现，这两种算法本质上都是采用 最大化目标策略 的思想。

什么是最大化目标策略？ 经过观察发现，无论是SARSA算法还是Q-Learning算法，它们的策略改进过程均可以表示为：

• 使用贪心策略，获取当前状态 S t S_t St​中最大状态-动作价值函数对应的动作： A ∗ = arg ⁡ max ⁡ a Q ( S t , a ) A^* = \mathop{\arg\max}\limits_{a} Q(S_t,a) A∗=aargmax​Q(St​,a)
• 在 A ∗ A^* A∗的基础上，再使用 ϵ − \epsilon- ϵ−贪心策略将 A ∗ A^* A∗转化为 软性策略： ∀ a ∈ A ( S t ) → π ( a ∣ S t ) = { 1 − ϵ k + ϵ k ∣ A ( S ) ∣ a = A ∗ ϵ k ∣ A ( S ) ∣ a ≠ A ∗ \begin{aligned} \forall a \in \mathcal A(S_t) \to \\ \pi(a \mid S_{t}) &= \left\{ \begin{array}{ll} 1 - \epsilon_k + \frac{\epsilon_k}{\mid\mathcal A(S) \mid} \quad a= A^*\\ \frac{\epsilon_k}{\mid\mathcal A(S) \mid}\quad\quad \quad \quad\quad a \neq A^* \end{array} \right. \end{aligned} ∀a∈A(St​)→π(a∣St​)​={1−ϵk​+∣A(S)∣ϵk​​a=A∗∣A(S)∣ϵk​​a=A∗​​

这种操作的本质是将估计值 Q ( S t , a ) Q(S_t,a) Q(St​,a)中的最大值作为 真实值的估计。这种估计结果会造成 Q ( S t , a ) Q(S_t,a) Q(St​,a)的估计结果与真实值的估计结果之间存在一个 正向偏差，这个偏差被称为 最大化偏差。

最大化偏差是如何出现的

再次观察上面描述策略改进过程：无论是选择最优动作 A ∗ A^* A∗还是将 A ∗ A^* A∗转化为软性策略 —— 根本就 没有偏差的机会：

• 选择最优动作 A ∗ → A^* \to A∗→ 选最大值；
• 软性策略转化 → \to → 基于人为设定 ϵ \epsilon ϵ的贪心算法；

因此，真正可能出现偏差的位置在策略评估过程——准确来说，就在状态-动作价值函数 Q ( S , A ) Q(S,A) Q(S,A)的 迭代过程。 因为策略评估中’动作a的选择‘仍然只是一个ε-贪心策略；和策略改进部分没有区别。

回顾SARSA和Q-Learning算法的迭代过程公式如下：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max ⁡ a Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)] \\ Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \mathop{\max}\limits_{a}Q(S_{t+1},a) - Q(S_t,A_t)] Q(St​,At​)←Q(St​,At​)+α[Rt+1​+γQ(St+1​,At+1​)−Q(St​,At​)]Q(St​,At​)←Q(St​,At​)+α[Rt+1​+γamax​Q(St+1​,a)−Q(St​,At​)]

我们发现：每个状态-动作价值函数 Q ( S , A ) Q(S,A) Q(S,A)都会选择选择下一时刻的最优状态-动作价值函数 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1​,At+1​)或者 max ⁡ a Q ( S t + 1 , a ) \mathop{\max}\limits_{a}Q(S_{t+1},a) amax​Q(St+1​,a)作为 Q ( S , A ) Q(S,A) Q(S,A)的更新方向。 即便SARSA选择的动作存在一定概率不是最优的，但下一时刻的动作也是通过ε-贪心策略选择出来的，因此，选择到最优动作的概率明显高于其他动作。

如果出现类似于 最优状态-动作价值函数是噪声或奖励结果(Reward)是满足某个分布的随机值时【传送门】

分析：如果出现这种情况会产生什么后果： 某一动作执行后，系统自动产生的随机奖励结果(Reward)和该动作本身 不匹配：

• 例如：在某状态 S ′ S' S′下，执行某动作 A ′ A' A′后的奖励结果不希望它太高；但通过奖励结果分布产生出的随机值导致该奖励结果过高——该结果直接影响 Q ( S ′ , A ′ ) Q(S',A') Q(S′,A′)的计算和后续迭代过程。

下面以Q-Learning为例，具体实现一下 随机奖励结果是如何对策略评估过程产生的影响的。

基于Q-Learning最大化偏差示例 示例环境介绍与问题描述

设计一个简易环境(Environment)：如下图所示： 其中： A A A表示一个状态(State)，该状态共包含两个动作(Action)：

A ( A ) = { a l e f t , a r i g h t } \mathcal A(A) = \{a_{left},a_{right}\} A(A)={aleft​,aright​}

B B B表示状态 A A A在执行动作 a l e f t a_{left} aleft​后转移的状态。该状态共包含 10个动作： A ( B ) = { a 1 , a 2 , . . . , a 10 } \mathcal A(B) = \{a_1,a_2,...,a_{10}\} A(B)={a1​,a2​,...,a10​} A A A状态执行 a l e f t a_{left} aleft​动作后，只能 唯一转移至 B B B状态 并且对应奖励 R l e f t = 0 R_{left} = 0 Rleft​=0； A A A状态执行 a r i g h t a_{right} aright​动作后，只能 唯一转移至 T e r m i n a l Terminal Terminal状态 并且对应奖励 R r i g h t = 0 R_{right} = 0 Rright​=0； B B B状态执行 A ( B ) → { a 1 , a 2 , . . . , a 10 } \mathcal A(B) \to \{a_1,a_2,...,a_{10}\} A(B)→{a1​,a2​,...,a10​}中的任意动作后，只能 唯一转移至 T e r m i n a l Terminal Terminal状态 并且各对应奖励 R 1 , R 2 , . . . , R 10 ∼ N ( − 0.01 , 1 ) R_1,R_2,...,R_{10} \sim \mathcal N(-0.01,1) R1​,R2​,...,R10​∼N(−0.01,1)； 该奖励服从均值为-0.01，方差为1的正态分布。

基于上述环境，提出的问题是：如果每次执行过程均以 A A A状态为初始状态， T e r m i n a l Terminal Terminal为终结状态，从初始状态 A A A出发，执行动作 a l e f t a_{left} aleft​的概率大一些还是执行动作 a r i g h t a_{right} aright​的概率大一些？

理论推导和真实环境之间的矛盾关系

观察：如果要更新状态-动作价值函数 Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)时，根据Q-Learning策略评估中 Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)的迭代公式： Q ( A , a l e f t ) ← Q ( A , a l e f t ) + α [ 0 + γ max ⁡ [ Q ( B , a 1 ) , Q ( B , a 2 ) , . . . , Q ( B , a 10 ) ] − Q ( A , a l e f t ) ] Q(A,a_{left}) \gets Q(A,a_{left}) + \alpha[0 + \gamma \mathop{\max}[Q(B,a_1),Q(B,a_2),...,Q(B,a_{10})] - Q(A,a_{left})] Q(A,aleft​)←Q(A,aleft​)+α[0+γmax[Q(B,a1​),Q(B,a2​),...,Q(B,a10​)]−Q(A,aleft​)] 如果尝试计算状态-动作价值函数 Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)的真实结果： 自然是使用‘贝尔曼期望方程’。 首先，将 Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)按照贝尔曼期望方程的形式展开： 上面提到：状态A执行动作left，只能唯一转移至B状态，并且奖励结果为0。因此‘动态特性函数’P(s’,r|s,a) = 1恒成立。 Q ( A , a l e f t ) = ∑ s ’ = B , R r i g h t = 0 P ( s ’ = B , R r i g h t = 0 ∣ s = A , a = a l e f t ) [ R r i g h t + γ V π ( B ) ] = 1 ⋅ [ 0 + γ V π ( B ) ] = γ V π ( B ) \begin{aligned} Q(A,a_{left}) & = \sum_{s’=B,R_{right}=0}P(s’=B,R_{right}=0 \mid s=A,a=a_{left})[R_{right} + \gamma V_{\pi}(B)] \\ & = 1 \cdot [0 + \gamma V_{\pi}(B)] \\ & = \gamma V_{\pi}(B) \end{aligned} Q(A,aleft​)​=s’=B,Rright​=0∑​P(s’=B,Rright​=0∣s=A,a=aleft​)[Rright​+γVπ​(B)]=1⋅[0+γVπ​(B)]=γVπ​(B)​ 继续使用贝尔曼期望方程计算 V π ( B ) V_{\pi}(B) Vπ​(B)的结果： B状态中包含10个动作，无论执行哪个动作，都会唯一转移至Terminal状态，并且奖励结果服从正态分布N(-0.01,1)。因此，同上，动态特性函数P(s’,r|s,a)=1恒成立。并且10个动作被选中的概率相同 -> 策略是等概率的均匀分布。 π ( a 1 ∣ B ) = π ( a 2 ∣ B ) = ⋯ = π ( a 10 ∣ B ) = 1 10 \pi(a_1 \mid B) = \pi(a_2 \mid B) = \cdots = \pi(a_{10} \mid B) = \frac{1}{10} π(a1​∣B)=π(a2​∣B)=⋯=π(a10​∣B)=101​ V π ( B ) = ∑ a ∈ A ( B ) π ( a ∣ B ) q π ( B , a ) = ∑ i = 1 10 π ( a i ∣ B ) q π ( B , a i ) = 1 10 ∑ i = 1 10 q π ( B , a i ) \begin{aligned} V_{\pi}(B) & = \sum_{a \in \mathcal A(B)}\pi(a \mid B)q_{\pi}(B,a) \\ & = \sum_{i=1}^{10} \pi(a_i \mid B)q_{\pi}(B,a_i) \\ & = \frac{1}{10} \sum_{i=1}^{10}q_{\pi}(B,a_i) \end{aligned} Vπ​(B)​=a∈A(B)∑​π(a∣B)qπ​(B,a)=i=1∑10​π(ai​∣B)qπ​(B,ai​)=101​i=1∑10​qπ​(B,ai​)​ 继续使用贝尔曼期望方程计算 q π ( B , a i ) q_\pi(B,a_i) qπ​(B,ai​)： R_i表示动作a_i执行后状态B转移至状态Terminal的奖励结果，因此动态特性函数P(s’,r|s,a)=1恒成立, R_i ~ N(-0.1,1)。 由于状态B执行任意动作后都会达到终止状态Terminal，因此回馈(Return)即奖励结果R_i。 q π ( B , a i ) = ∑ s ’ = T e r m i n a l , r = R i P ( s ’ = T e r m i n a l , r = R i ∣ s = B , a = a i ) [ R i ∣ s = B , a = a i ] = 1 ⋅ R i = R i \begin{aligned} q_{\pi}(B,a_i) & = \sum_{s’=Terminal,r=R_i}P(s’=Terminal,r=R_i \mid s=B,a=a_i)[R_i \mid s=B,a=a_i] \\ & = 1 \cdot R_i \\ & = R_i \end{aligned} qπ​(B,ai​)​=s’=Terminal,r=Ri​∑​P(s’=Terminal,r=Ri​∣s=B,a=ai​)[Ri​∣s=B,a=ai​]=1⋅Ri​=Ri​​ 将该结果带回上式： V π ( B ) = 1 10 ∑ i = 1 10 R i = R 1 + R 2 + ⋯ + R 10 10 = μ = − 0.01 Q ( A , a l e f t ) = γ ∗ V π ( B ) = − 0.01 × γ \begin{aligned} V_{\pi}(B) & = \frac{1}{10} \sum_{i=1}^{10}R_i = \frac{R_1 + R_2 + \cdots + R_{10}}{10} = \mu = -0.01 \\ Q(A,a_{left}) & = \gamma * V_{\pi}(B) = -0.01 \times \gamma \end{aligned} Vπ​(B)Q(A,aleft​)​=101​i=1∑10​Ri​=10R1​+R2​+⋯+R10​​=μ=−0.01=γ∗Vπ​(B)=−0.01×γ​ 因为 γ \gamma γ是衰减因子 → γ ∈ ( 0 , 1 ) \to \gamma \in (0,1) →γ∈(0,1)，因此： Q ( A , a l e f t ) = − 0.01 × γ < 0 Q(A,a_{left}) = -0.01 \times \gamma < 0 Q(A,aleft​)=−0.01×γ left,right self.state_a_action_num = 2 # state_b的action数量 self.state_b_action_num = nb # 初始状态 self.init_state = self.state_a # 还原为初始化操作： # state_a为初始状态 def reset_operation(self): self.state = self.state_a return self.state def step(self,action): # 初始化操作 reward = 10 done = None # 当前状态为state_a状态，执行动作left; if self.state == self.state_a and action == self.left: # 状态转移过程由state_a转移到state_b self.state = self.state_b # state_a -> state_b的奖励结果 reward = 0 # 是否达到最终状态 done = False # 当前状态为state_a状态，执行动作right; elif self.state == self.state_a and action == self.right: self.state = self.state_terminal reward = 0 done = True # 当前状态为state_b状态，执行一个动作，直接到达state_terminal elif self.state == self.state_b: reward = round(random.normalvariate(self.mu,self.sigma),2) done = True return self.state,reward,done

初始化 Q − T a b l e Q-Table Q−Table： 这里的Q-Table使用字典嵌套的形式，因为不同状态下存在各自有意义的动作。

def init_q_table(env):

    # 初始化Q_table
    Q = {
        env.state_a:{action:0 for action in range(env.state_a_action_num)},
        env.state_b:{action:0 for action in range(env.state_b_action_num)},
        env.state_terminal: {action: 0 for action in range(env.state_a_action_num)}
    }
    return Q

在状态确定的条件下，使用 ϵ − \epsilon- ϵ−贪心策略对动作进行选择：

def select_action_from_behavoiur_policy(action_value_dict,epsilon):

    # 以(1- epsilon)的概率，选择当前状态下 [状态-动作价值函数最大值对应的动作];
    # random.random() -> 在(0,1)均匀分布中随机抽取1个点，和epsilon比较大小;
    # random.random()结果大于epsilon的概率 -> 1 - epsilon;
    if random.random() > epsilon:
        # 可能存在[状态-动作价值函数相同]并且都是最大值
        max_keys = [key for key, value in action_value_dict.items() if value == max(action_value_dict.values())]
        # 从中任意选择一个[动作]
        action = random.choice(max_keys)
    else:
        # 在Q-Table中对应state中随机抽取一个动作 -> 每个动作被选择的概率均相同;
        action = random.sample(action_value_dict.keys(),1)[0]
    return action

构建Q-Learning算法的迭代过程：

def q_learning(env,alpha=0.2,num_of_episode=1000, gamma=0.9,epsilon=0.2):

    Q = init_q_table(env)
    Record = {
        env.state_a: {action: [] for action in range(env.state_a_action_num)},
        env.state_b: {action: [] for action in range(env.state_b_action_num)},
        env.state_terminal: {action: [] for action in range(env.state_a_action_num)}
    }
    select_l = []

    for num in range(num_of_episode):
        # 初始化状态S
        state = env.reset_operation()
        count = 0
        while True:
            count += 1
            action = select_action_from_behavoiur_policy(Q[state],epsilon)
            next_state,reward,done = env.step(action)
            max_value = random.choice([value for action,value in Q[next_state].items() if value == max(Q[next_state].values())])
            Q[state][action] += alpha * (reward + gamma * max_value - Q[state][action])
            Record[state][action].append(Q[state][action])
            if done:
                break
            else:
                state = next_state
        if count > 1:
            select_l.append(1)
        else:
            select_l.append(0)
    return Q,Record,select_l

实验过程 实验一：观察 Q ( A , a l e f t ) , Q ( A , a r i g h t ) Q(A,a_{left}),Q(A,a_{right}) Q(A,aleft​),Q(A,aright​)迭代过程中的变化情况

重复执行1000次Q-Learning算法，观察状态 A A A对应的2个状态-动作价值函数 Q ( A , a l e f t ) , Q ( A , a r i g h t ) Q(A,a_{left}),Q(A,a_{right}) Q(A,aleft​),Q(A,aright​)在迭代过程中的变化情况：

if __name__ == '__main__':
    env = Env(-0.1, 1, 10)
    Q_table, Record, select_l = q_learning(env, num_of_episode=1000)
    for action,change_l in Record[0].items():
        x = [i for i in range(len(change_l))]
        plt.scatter(x,change_l,s=2)
    plt.show()

返回结果如下： 由于正态分布生成结果的随机性，因此返回结果并不是每一次都是相同的，但趋势基本是相似的。 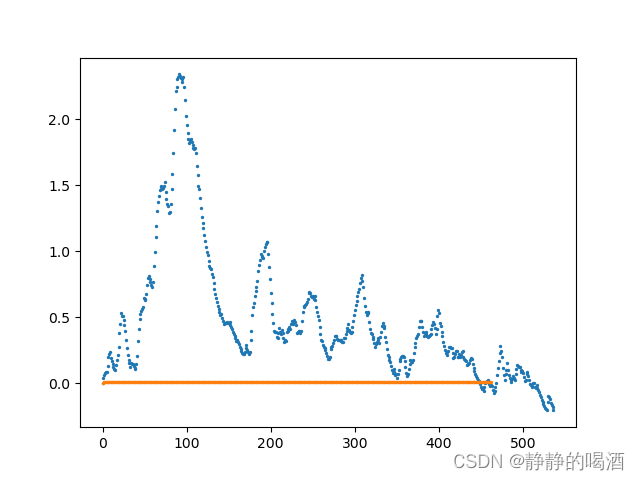观察上图：

本次试验一共执行了1000次Q-Learning。橙色点 表示 Q ( A , a r i g h t ) Q(A,a_{right}) Q(A,aright​)的变化过程(注意，橙色点并不是全部是0，只是变化得非常小)；蓝色点 表示 Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)的变化过程。 我们发现：

• 在迭代开始初期，由于正态分布生成的正向结果以及Q-Learning的贪心策略，导致 Q ( A , a r i g h t ) Q(A,a_{right}) Q(A,aright​)没有竞争力，导致前面几百次试验选择的动作基本是 Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)。
• 到达试验的中后期， Q ( A , a l e f t ) Q(A,a_{left}) Q(A,aleft​)的结果逐渐下降，直到 Q ( A , a l e f t ) < Q ( A , a r i g h t ) Q(A,a_{left})