最大化偏差问题与Double Q-Learning(二)——消除最大化偏差的具体方法

目录

上一节介绍了最大化偏差(Maximization Bias)的产生原因，本节将介绍消除最大化偏差的具体方法。

回顾 最大化偏差

最大化偏差产生的 核心原因 在于使用 贪心算法 对下一时刻的状态-动作价值函数 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)进行估计时，该估计结果中包含较大权重的噪声/该估计结果本身就是噪声 → \to → 导致 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)将误差较大的信息进行增量更新，进而影响后续迭代过程中动作的选择。

Q-Learning的算法缺陷

Q-Learning算法使用 max ⁡ a Q ( S t + 1 , a ) \mathop{\max}\limits_{a}Q(S_{t+1},a) amax​Q(St+1​,a)的方式来更新 S t + 1 S_{t+1} St+1​状态下的最优状态-动作价值函数。这种求解方式实际上是一种 比较武断的做法：

回顾Q-Learning算法的动量更新过程： Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max ⁡ a Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \mathop{\max}\limits_{a}Q(S_{t+1},a) - Q(S_t,A_t)] Q(St​,At​)←Q(St​,At​)+α[Rt+1​+γamax​Q(St+1​,a)−Q(St​,At​)] 可以将 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)每一次更新过程理解为 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)从当前位置朝 max ⁡ a Q ( S t + 1 , a ) \mathop{\max}\limits_{a}Q(S_{t+1},a) amax​Q(St+1​,a)方向的偏移过程。 整个偏移过程按顺序 分为2个步骤：

• 对 S t + 1 S_{t+1} St+1​状态下最大的状态-动作价值函数 max ⁡ a Q ( S t + 1 , a ) \mathop{\max}\limits_{a}Q(S_{t+1},a) amax​Q(St+1​,a)进行求解；
• 计算 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)与 max ⁡ a Q ( S t + 1 , a ) \mathop{\max}\limits_{a}Q(S_{t+1},a) amax​Q(St+1​,a)之间的偏差信息，使用增量更新方式将该偏差信息对 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)进行更新；

该过程本质上是先求解最大值，再基于最大值求解期望的过程。 但该过程存在 思路上的缺陷：将最大值与最优值划等号。

• 本意是从 S t + 1 S_{t+1} St+1​状态下计算所有动作的 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)的期望( S t + 1 S_{t+1} St+1​状态各动作期望的偏移方向)，再从中挑选一个最优值(最优方向)作为 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)的偏移方向 → \to → 先求解期望，再基于期望求解最大值。
• 但Q-Learning算法的操作正好相反——因此在最大值替代最优值的过程中出现了 最大化偏差，从而出现对更新后的 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)产生过估计(overestimation)现象。

对 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)的过估计现象本身可能不会使算法失败，但可能会使收敛速度变慢，甚至可能会提前收敛。最终导致估计结果与真实结果之间存在差距。

过估计(overestimation)

举一个简单例子描述过估计。 已知 一组数字集合 X \mathcal X X，集合内各元素独立同分布。对该集合执行如下操作：

• 假设 x ′ x' x′是 X \mathcal X X中数值最大的元素，即 x ′ = max ⁡ ( X ) x' = \max(\mathcal X) x′=max(X)。对 x ′ x' x′求解期望： x'是一个普通常数，其期望就是本身。 max ⁡ ( X ) = E [ max ⁡ ( X ) ] \max(\mathcal X)=\mathbb E[\max(\mathcal X)] max(X)=E[max(X)]
• 假设 E [ X ] \mathbb E[\mathcal X] E[X]表示数字集合 X \mathcal X X的期望： 集合内各元素独立同分布 -> 各元素被选择的概率相同 -> 1 N \frac{1}{N} N1​ E [ X ] = 1 N ∑ i = 1 N x i \mathbb E[\mathcal X] = \frac{1}{N}\sum_{i=1}^N x_i E[X]=N1​i=1∑N​xi​ 对 E [ X ] \mathbb E[\mathcal X] E[X]求解最大值： E(X)本身是一个均值(常数)，该集合只有它一个元素，最大值就是本身。 max ⁡ ( E [ X ] ) = E [ X ] \max (\mathbb E[\mathcal X]) = \mathbb E[\mathcal X] max(E[X])=E[X] 又因为 max ⁡ ( X ) ≥ E [ X ] \max(\mathcal X) \geq \mathbb E[\mathcal X] max(X)≥E[X]恒成立(贝尔曼最优方程中介绍过最大值与期望值的关系)，则有： E [ max ⁡ ( X ) ] = max ⁡ ( X ) ≥ E [ X ] = max ⁡ ( E [ X ] ) E [ max ⁡ ( X ) ] ≥ max ⁡ ( E [ X ] ) \begin{aligned} \mathbb E[\max(\mathcal X)] = \max(\mathcal X)& \geq \mathbb E[\mathcal X] = \max (\mathbb E[\mathcal X]) \\ \mathbb E[\max(\mathcal X)] & \geq \max (\mathbb E[\mathcal X]) \end{aligned} E[max(X)]=max(X)E[max(X)]​≥E[X]=max(E[X])≥max(E[X])​ 而最大化偏差(Maximization Bias)即： E [ max ⁡ ( X ) ] − max ⁡ ( E [ X ] ) > 0 \mathbb E[\max(\mathcal X)] - \max (\mathbb E[\mathcal X]) > 0 E[max(X)]−max(E[X])>0

如何解决过估计现象 单估计器方法(Single Estimator)

既然 E [ max ⁡ ( X ) ] \mathbb E[\max(\mathcal X)] E[max(X)]在估计过程中产生了最大化偏差，干脆 使用 max ⁡ ( E [ X ] ) \max (\mathbb E[\mathcal X]) max(E[X]) 直接替换 E [ max ⁡ ( X ) ] \mathbb E[\max(\mathcal X)] E[max(X)]。 新的问题：我们要如何求解 max ⁡ E [ X ] \max \mathbb E[\mathcal X] maxE[X] → \to → 单估计器方法(Single Estimator)。

单估计器方法通过大量采样得到一个关于 E [ X ] \mathbb E[\mathcal X] E[X]的近似采样集合——通过对集合中的元素取最大值来近似 max ⁡ ( E [ X ] ) \max (\mathbb E[\mathcal X]) max(E[X])。

max ⁡ ( E [ X ] ) ≈ max ⁡ { E [ X 1 ] , E [ X 2 ] , ⋯   , E [ X N ] } ( X 1 , X 2 , ⋯   , X N ⊂ X ) \max (\mathbb E[\mathcal X]) \approx \max\{\mathbb E[\mathcal X_1],\mathbb E[\mathcal X_2],\cdots,\mathbb E[\mathcal X_N]\}(\mathcal X_1,\mathcal X_2,\cdots,\mathcal X_N \subset \mathcal X) max(E[X])≈max{E[X1​],E[X2​],⋯,E[XN​]}(X1​,X2​,⋯,XN​⊂X) 继续使用最大化偏差问题与Double Q-Learning(一)——最大化偏差问题介绍中的例子，对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)最优值的估计过程设计如下： 由于示例中 Q − T a b l e Q-Table Q−Table中只有 A , B A,B A,B两个状态存在状态-动作价值函数的更新，并且：

• Q − T a b l e Q-Table Q−Table中状态 A A A包含2个元素 → Q ( A , a l e f t ) , Q ( A , a r i g h t ) \to Q(A,a_{left}),Q(A,a_{right}) →Q(A,aleft​),Q(A,aright​)
• Q − T a b l e Q-Table Q−Table中状态 B B B包含10个元素 → Q ( B , a 1 ) , Q ( B , a 2 ) , ⋯   , Q ( B , a 10 ) \to Q(B,a_1),Q(B,a_2),\cdots,Q(B,a_{10}) →Q(B,a1​),Q(B,a2​),⋯,Q(B,a10​)

基于下一时刻状态 S t + 1 S_{t+1} St+1​，对样本为 Q − T a b l e Q-Table Q−Table中 S t + 1 S_{t+1} St+1​状态对应的 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a) 重复进行 N N N次采样：

• 每次采样之间相互独立；
• 每次采出的 样本数量 是对应 Q − T a b l e Q-Table Q−Table中状态对应元素数量的子集；
• 将每次采出的样本取期望——期望结果作为一个随机变量；
• N N N次采样对应 N N N个随机变量——取 N N N个随机变量的最大值。

具体代码如下： 这里设置采样次数 N = 20 N=20 N=20。

• 如果 S t + 1 S_{t+1} St+1​状态是状态 B B B → \to → 状态 B B B的 Q − T a b l e Q-Table Q−Table中每次采样都随机抽取80%的元素求解期望，最终从20个期望样本中获取最大值作为 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)；
• 如果 S t + 1 S_{t+1} St+1​状态是状态 A A A → \to → 直接求解期望——因为 A A A状态对应的 Q − T a b l e Q-Table Q−Table元素只有2个，太少了；

在本节最后附上完整过程代码。

def single_estimater_operation(Q,next_state):

    value_l = [i for i in Q[next_state].values()]
    sample_l = []
    if len(value_l) > 2:
        for _ in range(20):
            random.shuffle(value_l)
            sample_l.append(sum(value_l[:int(len(value_l) * 0.8)]) / int(len(value_l) * 0.8))
    else:
    	# 该步骤就是求期望，sample_l中的元素全部是相同的，主要是因为状态A的动作只有2个，太少了；
        sample_l.append(sum(value_l[:len(value_l)]) / len(value_l))
    return max(sample_l)

重新观察Q-Learning方法与Single Estimator方法对于状态 A A A条件下对动作 { a l e f t , a r i g h t } \{a_{left},a_{right}\} {aleft​,aright​}选择概率进行比较。比较结果如下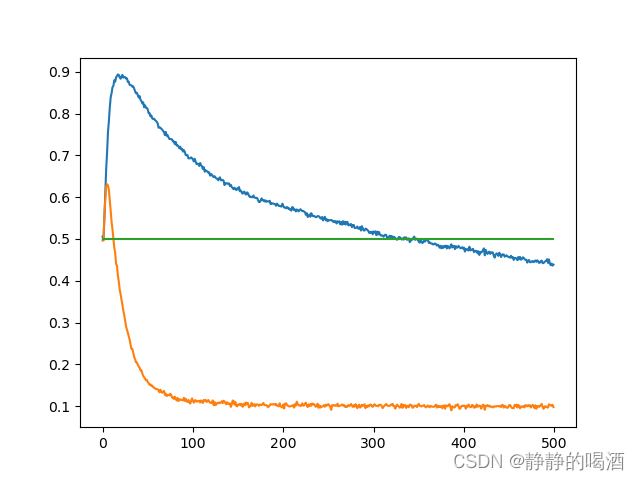： 其中 橙色线 表示Single Estimator方法选择概率的变化，蓝色线 表示Q-Learning方法选择概率的变化。在迭代开始初期，Single Estimator方法仍然倾向于选择 a l e f t a_{left} aleft​,但相比于Q-Learning方法，它能在更短的迭代次数中将最大化偏差消除掉。

该方式本质上是通过采样对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)进行近似操作，是对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)的 无偏估计。这种无偏估计操作是针对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)元素过多的情况，如果 Q − T a b l e Q-Table Q−Table内 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)元素有限，可以通过直接求解 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)元素期望的方式进行无偏估计： max ⁡ a Q ( S t + 1 , a ) ≈ ∑ a π ( a ∣ S t + 1 ) Q ( S t + 1 , a ) \mathop{\max}\limits_{a} Q(S_{t+1},a) \approx \sum_{a}\pi(a \mid S_{t+1})Q(S_{t+1},a) amax​Q(St+1​,a)≈a∑​π(a∣St+1​)Q(St+1​,a) 对应的 Q ( S t , A t ) Q(S_{t},A_{t}) Q(St​,At​)迭代公式如下： Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ ∑ a π ( a ∣ S t + 1 ) Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \sum_{a}\pi(a \mid S_{t+1})Q(S_{t+1},a) - Q(S_t,A_t)] Q(St​,At​)←Q(St​,At​)+α[Rt+1​+γa∑​π(a∣St+1​)Q(St+1​,a)−Q(St​,At​)] 很明显，这就是期望SARSA的迭代公式。期望SARSA的具体代码如下：

def get_expected_value(Q,next_state):

    value_l = [i for i in Q[next_state].values()]
    return sum(value_l) / len(value_l)

返回图像结果如下：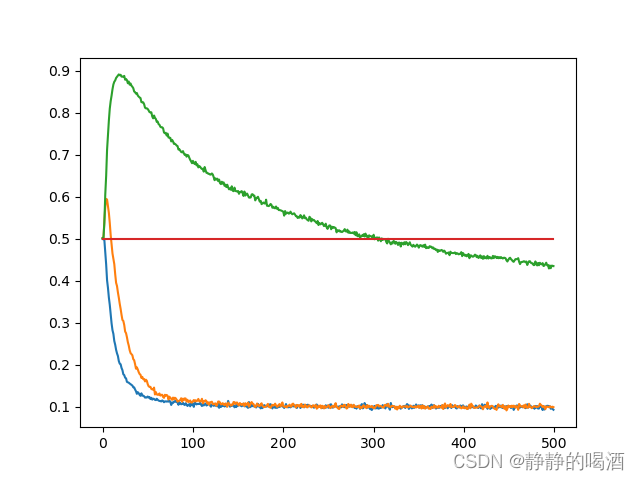

其中，蓝色线 表示期望SARSA结果；橙色线 表示单估计器方法结果；观察图像可以看出，蓝色线从迭代开始时选择 a r i g h t a_{right} aright​的概率迅速提升，几乎完全消除了最大化偏差。相比于单估计器方法效果更好。

因此，期望SARSA方法本身就是单估计器方法的一种特例。单估计器方法实现的无偏估计结果，其误差仅由随机选取样本过程中的方差组成；但期望SARSA在每次迭代过程中直接使用样本的完整期望进行更新，将单估计器方法中的方差有效地消除掉，从而得到准确度更高的迭代过程。

附：完整代码示例

import numpy as np
import random
import matplotlib.pyplot as plt
from tqdm import trange


class Env():

    # 构造环境
    def __init__(self, mu, sigma, nb):

        self.mu = mu
        self.sigma = sigma

        # state 信息
        self.state_a = 0
        self.state_b = 1
        self.state_terminal = 2

        # action 信息(离散型随机变量)
        self.left = 0
        self.right = 1

        # 状态数量 -> state_a,state_b,state_terminal
        self.num_state = 3
        # state_a的action数量 -> left,right
        self.state_a_action_num = 2
        # state_b的action数量
        self.state_b_action_num = nb
        # 初始状态
        self.init_state = self.state_a

    # 还原为初始化操作：
    # state_a为初始状态
    def reset_operation(self):
        self.state = self.state_a
        return self.state

    def step(self, action):

        # 初始化操作
        reward = 10
        done = None
        # 当前状态为state_a状态，执行动作left;
        if self.state == self.state_a and action == self.left:
            # 状态转移过程由state_a转移到state_b
            self.state = self.state_b
            # state_a -> state_b的奖励结果
            reward = 0
            # 是否达到最终状态
            done = False

        # 当前状态为state_a状态，执行动作right;
        elif self.state == self.state_a and action == self.right:
            self.state = self.state_terminal
            reward = 0
            done = True

        # 当前状态为state_b状态，执行一个动作，直接到达state_terminal
        elif self.state == self.state_b:
            reward = round(random.normalvariate(self.mu, self.sigma), 2)
            done = True

        return self.state, reward, done

def init_q_table(env):

    # 初始化Q_table
    Q = {
        env.state_a:{action:0 for action in range(env.state_a_action_num)},
        env.state_b:{action:0 for action in range(env.state_b_action_num)},
        env.state_terminal: {action: 0 for action in range(env.state_a_action_num)}
    }
    return Q

def select_action_from_behavoiur_policy(action_value_dict,epsilon):

    # 以(1- epsilon)的概率，选择当前状态下 [状态-动作价值函数最大值对应的动作];
    # random.random() -> 在(0,1)均匀分布中随机抽取1个点，和epsilon比较大小;
    # random.random()结果大于epsilon的概率 -> 1 - epsilon;
    if random.random() > epsilon:
        # 可能存在[状态-动作价值函数相同]并且都是最大值
        max_keys = [key for key, value in action_value_dict.items() if value == max(action_value_dict.values())]
        # 从中任意选择一个[动作]
        action = random.choice(max_keys)
    else:
        # 在Q-Table中对应state中随机抽取一个动作 -> 每个动作被选择的概率均相同;
        action = random.sample(action_value_dict.keys(),1)[0]
    return action

def get_expected_value(Q,next_state):

    value_l = [i for i in Q[next_state].values()]
    return sum(value_l) / len(value_l)

def single_estimater_operation(Q,next_state,sample_num):

    value_l = [i for i in Q[next_state].values()]
    sample_l = []
    if len(value_l) > 2:
        for _ in range(sample_num):
            random.shuffle(value_l)
            sample_l.append(sum(value_l[:int(len(value_l) * 0.8)]) / int(len(value_l) * 0.8))
    else:
        sample_l.append(sum(value_l[:len(value_l)]) / len(value_l))

    return max(sample_l)

def hybrid_algorithm(env,single_estimater_sample_num=10,mode="q_learning",alpha=0.2,num_of_episode=1000, gamma=0.9,epsilon=0.2):
    Q = init_q_table(env)
    Record = {
        env.state_a: {action: [] for action in range(env.state_a_action_num)},
        env.state_b: {action: [] for action in range(env.state_b_action_num)},
        env.state_terminal: {action: [] for action in range(env.state_a_action_num)}
    }
    select_l = []
    assert mode in ["q_learning","expected_SARSA","single_estimater"]

    for num in range(num_of_episode):

        state = env.reset_operation()
        count = 0
        while True:
            count += 1
            action = select_action_from_behavoiur_policy(Q[state],epsilon)
            next_state,reward,done = env.step(action)

            # expected_SARSA
            if mode == "expected_SARSA":
                expected_value = get_expected_value(Q,next_state)
                Q[state][action] += alpha * (reward + gamma * expected_value - Q[state][action])
            # q_learning operation
            elif mode == "q_learning":
                max_value = random.choice([value for action, value in Q[next_state].items() if value == max(Q[next_state].values())])
                Q[state][action] += alpha * (reward + gamma * max_value - Q[state][action])
            # single_estimater
            else:
                approx_value = single_estimater_operation(Q,next_state,single_estimater_sample_num)
                Q[state][action] += alpha * (reward + gamma * approx_value - Q[state][action])

            Record[state][action].append(Q[state][action])
            if done:
                break
            else:
                state = next_state
        if count > 1:
            select_l.append(1)
        else:
            select_l.append(0)
    return Q, Record, select_l


if __name__ == '__main__':
    env = Env(-0.1, 1, 10)
    # Q_table, Record, select_l = expected_SARSA(env, num_of_episode=1000)
    # for action,change_l in Record[0].items():
    #     x = [i for i in range(len(change_l))]
    #     plt.scatter(x,change_l,s=2)
    # plt.show()

    stat_l_sarsa = []
    stat_l_single_estimator = []
    stat_q_learning = []

    for i in trange(10000):
        # Q_table, Record, select_l = hybrid_algorithm(env, num_of_episode=500)
        _, _, select_l_sarsa = hybrid_algorithm(env, mode="expected_SARSA", num_of_episode=500)
        _, _, select_l_single_estimator = hybrid_algorithm(env,mode="single_estimater", num_of_episode=500)
        _, _, select_l_q_learning = hybrid_algorithm(env, mode="q_learning", num_of_episode=500)

        stat_l_sarsa.append(select_l_sarsa)
        stat_l_single_estimator.append(select_l_single_estimator)
        stat_q_learning.append(select_l_q_learning)

    k_sarsa = np.array(stat_l_sarsa)
    k_single = np.array(stat_l_single_estimator)
    k_q = np.array(stat_q_learning)
    x = [i for i in range(500)]
    plt.plot(x, np.mean(k_sarsa, axis=0))
    plt.plot(x,np.mean(k_single,axis=0))
    plt.plot(x, np.mean(k_q, axis=0))
    plt.plot(x, [0.5 for _ in x])
    plt.show()

下一节将介绍处理最大化偏差的其他方法。

相关参考： 深度强化学习系列(5): Double Q-Learning原理详解 解剖[强化学习]Double Learning本质并对比Q-Learning与期望Sarsa——宫商角徵羽​ 深度强化学习原理、算法pytorch实战 —— 刘全，黄志刚编著