最大化偏差问题与Double Q-Learning(三)——双估计器方法与Double Q-Learning

目录

上一节介绍了使用单估计器方法(Single Estimator)处理最大化偏差(Maximization Bias)现象，本节将介绍基于双估计器方法(Double Estimator)处理最大化偏差问题。 附上论文原文链接

回顾 单估计器(Single Estimator)方法

由于Q-Learning算法中出现的 最优值即最大值 思路上的缺陷，导致了过估计(overestimate)现象的发生。 Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max ⁡ a Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha [R_{t+1} + \gamma \mathop{\max}\limits_{a} Q(S_{t+1},a) - Q(S_t,A_t)] Q(St​,At​)←Q(St​,At​)+α[Rt+1​+γamax​Q(St+1​,a)−Q(St​,At​)] 而单估计器方法的核心是通过采样获取最大期望的价值函数近似当前步骤的最优结果，从而达到对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)无偏估计的目的。具体流程如下：

• 重复执行 N N N次采样——各采样之间相互独立( s i ( i = 1 , 2 , ⋯   , N ) s_i(i =1,2,\cdots,N) si​(i=1,2,⋯,N)表示每一次采样得到的样本集合)； S = { s 1 , s 2 , ⋯   , s N } \mathcal S = \{s_1,s_2, \cdots ,s_N\} S={s1​,s2​,⋯,sN​}
• 每次采出的样本数量是对应 Q − T a b l e Q-Table Q−Table中状态对应元素数量的 子集； s i ∈ Q ( S t + 1 , a ) ( i = 1 , 2 , ⋯   , N ) s_i \in Q(S_{t+1},a)(i=1,2,\cdots,N) si​∈Q(St+1​,a)(i=1,2,⋯,N)
• 对每次采出的样本求解期望——期望结果作为一个随机变量； 由于各样本间相互独立，因此求期望过程中各样本的概率相等。 E [ s i ] = 1 ∣ s i ∣ ∑ s ∈ s i s ( i = 1 , 2 , ⋯   , N ) \mathbb E[s_i] = \frac{1}{\mid s_i \mid} \sum_{s \in s_i} s (i = 1,2,\cdots,N) E[si​]=∣si​∣1​s∈si​∑​s(i=1,2,⋯,N)
• N N N次采样对应 N N N个随机变量——求解 N N N个随机变量的最大值，并将最大值进行增量更新操作； E [ S ] = max ⁡ { E [ s 1 ] , E [ s 2 ] , ⋯   , E [ s N ] } Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ E [ S ] − Q ( S t , A t ) ] \mathbb E[\mathcal S] = \max\{\mathbb E[s_1],\mathbb E[s_2],\cdots,\mathbb E[s_N]\} \\ Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha [R_{t+1} + \gamma \mathbb E[\mathcal S] - Q(S_t,A_t)] E[S]=max{E[s1​],E[s2​],⋯,E[sN​]}Q(St​,At​)←Q(St​,At​)+α[Rt+1​+γE[S]−Q(St​,At​)]

该方法的核心思想是通过 采样 + 求期望 操作实现对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)的 无偏估计，将误差控制在随机选取样本过程中的方差部分，从而得到更稳定、准确度更高的迭代过程。

期望SARSA方法

期望SARSA可以理解成单估计器方法的一种特殊情况，相比于单估计器方法，它直接省去了 采样过程：

• 直接使用 Q − T a b l e Q-Table Q−Table中 S t + 1 S_{t+1} St+1​状态下的所有状态-动作价值函数 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)求解期望； E π ( a ∣ S t + 1 ) [ Q ( S t + 1 , a ∣ S t + 1 ) ] = ∑ i = 1 N π ( a t + 1 ( i ) ∣ s S t + 1 ) Q ( S t + 1 , a t + 1 ( i ) ) \mathbb E_{\pi(a \mid S_{t+1})}[Q(S_{t+1},a \mid S_{t+1})] = \sum_{i=1}^N \pi(a_{t+1}^{(i)} \mid sS_{t+1})Q(S_{t+1},a_{t+1}^{(i)}) Eπ(a∣St+1​)​[Q(St+1​,a∣St+1​)]=i=1∑N​π(at+1(i)​∣sSt+1​)Q(St+1​,at+1(i)​)
• 将期望结果使用增量更新方式对 Q ( S t , A t ) Q(S_{t},A_t) Q(St​,At​)进行迭代； Q ( S t , A t ) ← Q ( S t , A t ) + α ( R t + 1 + γ E π ( a ∣ S t + 1 ) [ Q ( S t + 1 , a ∣ S t + 1 ) ] − Q ( S t , A t ) ) Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha(R_{t+1} + \gamma \mathbb E_{\pi(a \mid S_{t+1})}[Q(S_{t+1},a \mid S_{t+1})] - Q(S_t,A_t)) Q(St​,At​)←Q(St​,At​)+α(Rt+1​+γEπ(a∣St+1​)​[Q(St+1​,a∣St+1​)]−Q(St​,At​))

该操作与单估计器方法的核心区别在于：

• 无需收集由样本子集期望构成的随机变量集合；
• 无需获取最大值——当某一时刻 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)确定的情况下，期望结果也是唯一确定的。

相比于单估计器方法，期望SARSA方法直接对整个 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)中的所有状态-动作价值函数求解期望以实现对 Q ( S t + 1 , a ) Q(S_{t+1},a) Q(St+1​,a)的 无偏估计，从而使期望结果中方差的影响消除的更加彻底，迭代过程更加稳定。 完整代码见传送门

双估计器方法(Double Estimator) 单估计器方法的缺陷

回顾最大化偏差问题与Double Q-Learning(二)——消除最大化偏差的具体方法中单估计器方法与Q-Learning方法对比结果图像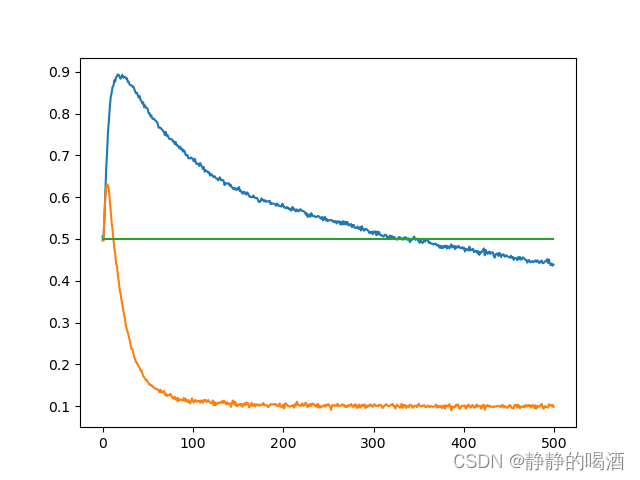： 其中纵坐标表示在 A A A状态下，选择动作 { a l e f t , a r i g h t } \{a_{left},a_{right}\} {aleft​,aright​}对应的概率大小，横坐标表示 Q − T a b l e Q-Table Q−Table的迭代次数。发现虽然单估计器方法(橙色线) 相比于 Q-Learning方法(蓝色线)能够更好地处理最大化偏差问题，但迭代初期依然存在少量过估计(overestimate)现象。

为了减少单估计器方法的最大化偏差影响，介绍一种双估计器方法处理迭代过程中的高估计。

双估计器方法的思路过程 场景构建

构建一个场景来描述双估计器方法的执行过程： 已知一组包含 M M M个随机变量的随机变量集合 X \mathcal X X表示如下： X = { x 1 , x 2 , ⋯   , x M } \mathcal X = \{x_1,x_2,\cdots,x_M\} X={x1​,x2​,⋯,xM​} 最终目标是求解随机变量集合 X \mathcal X X中变量 x i x_i xi​的最大期望结果。即： max ⁡ i E [ x i ] \mathop{\max}\limits_{i} \mathbb E[x_i] imax​E[xi​] 针对目标 max ⁡ i E [ x i ] \mathop{\max}\limits_{i} \mathbb E[x_i] imax​E[xi​]，对随机变量集合 X \mathcal X X进行采样： S = ⋃ i = 1 M s i S ← { s 1 , s 2 , ⋯   , s M } \mathcal S = \bigcup_{i=1}^M s_i \\ \mathcal S \gets \{s_1,s_2,\cdots,s_M\} S=i=1⋃M​si​S←{s1​,s2​,⋯,sM​} 其中 s i ∣ i = 1 M s_i \mid_{i=1}^M si​∣i=1M​表示随机变量集合中的元素 x i x_i xi​对应的 样本集合。 注意，这里说的是‘样本集合’，而不是‘单个样本’。 定义两个 估计器 μ A , μ B \mu^A,\mu^B μA,μB： μ A = { μ 1 A , μ 2 A , ⋯   , μ M A } μ B = { μ 1 B , μ 2 B , ⋯   , μ M B } \mu^A = \{\mu^A_1,\mu^A_2,\cdots,\mu^A_M\} \\ \mu^B = \{\mu^B_1,\mu^B_2,\cdots,\mu^B_M\} μA={μ1A​,μ2A​,⋯,μMA​}μB={μ1B​,μ2B​,⋯,μMB​} 这里强调一下估计器的作用：使用估计器 μ i \mu_i μi​进行采样得到样本集合 s i s_i si​，再通过样本集合 s i s_i si​估计随机变量 x i x_i xi​。

基于单个随机变量 x 1 x_1 x1​示例双估计器过程

以 随机变量 x 1 x_1 x1​的视角 为例，具体执行过程如下：

• 对随机变量 x 1 x_1 x1​使用估计器进行采样，得到样本集合 s 1 s_1 s1​。设样本集合中一共包含数量为 ∣ s 1 ∣ \mid s_1\mid ∣s1​∣ 的样本，数学符号表示如下： s 1 = { s 1 ( 1 ) , s 1 ( 2 ) , ⋯   , s 1 ( ∣ s 1 ∣ ) } s_1 = \{s_1^{(1)},s_1^{(2)},\cdots,s_1^{(\mid s_1\mid)}\} s1​={s1(1)​,s1(2)​,⋯,s1(∣s1​∣)​}
• 假设 s 1 s_1 s1​样本集内存在 ∣ s 1 ( A ) ∣ \mid s_1^{(A)}\mid ∣s1(A)​∣个样本是由 μ 1 A \mu^A_1 μ1A​估计器采集的结果，剩余 ∣ s 1 ( B ) ∣ \mid s_1^{(B)}\mid ∣s1(B)​∣个样本是由 μ 1 B \mu^B_1 μ1B​采集的结果，两种集合分别命名为 s 1 ( A ) , s 1 ( B ) s_1^{(A)},s_1^{(B)} s1(A)​,s1(B)​。 s 1 ( A ) s_1^{(A)} s1(A)​与 s 1 ( B ) s_1^{(B)} s1(B)​的具体关系表示如下： s 1 ( A ) ∪ s 1 ( B ) = s 1 s 1 ( A ) ∩ s 1 ( B ) = ∅ ∣ s 1 ( A ) ∣ + ∣ s 1 ( B ) ∣ = ∣ s 1 ∣ s_1^{(A)} \cup s_1^{(B)} = s_1 \\ s_1^{(A)} \cap s_1^{(B)} = \emptyset \\ \mid s_1^{(A)}\mid + \mid s_1^{(B)}\mid = \mid s_1\mid s1(A)​∪s1(B)​=s1​s1(A)​∩s1(B)​=∅∣s1(A)​∣+∣s1(B)​∣=∣s1​∣
• 设定一个新的符号： μ 1 A ( S ) \mu_1^{A}(S) μ1A​(S)，它表示 针对随机变量元素 x 1 x_1 x1​对应在估计器 μ 1 A \mu_1^A μ1A​采样的样本集合 s 1 ( A ) s_1^{(A)} s1(A)​的期望结果。数学表示如下： μ 1 A ( S ) = 1 ∣ s 1 ( A ) ∣ ∑ s ∈ s 1 ( A ) s = E { μ 1 A } \mu_1^{A}(S) = \frac{1}{\mid s_1^{(A)}\mid}\sum_{s \in s_1^{(A)}} s = \mathbb E\{\mu_1^{A}\} μ1A​(S)=∣s1(A)​∣1​s∈s1(A)​∑​s=E{μ1A​} 同理，新的符号： μ 1 B ( S ) \mu_1^{B}(S) μ1B​(S)，它表示 针对随机变量元素 x 1 x_1 x1​对应在估计器 μ 1 B \mu_1^B μ1B​采样的样本集合 s 1 ( B ) s_1^{(B)} s1(B)​的期望结果。 μ 1 B ( S ) = 1 ∣ s 1 ( B ) ∣ ∑ s ∈ s 1 ( B ) s = E { μ 1 B } \mu_1^{B}(S) = \frac{1}{\mid s_1^{(B)}\mid}\sum_{s \in s_1^{(B)}} s = \mathbb E\{\mu_1^{B}\} μ1B​(S)=∣s1(B)​∣1​s∈s1(B)​∑​s=E{μ1B​}

至此，随机变量 x 1 x_1 x1​分别在估计器 μ 1 A , μ 1 B \mu^A_1,\mu^B_1 μ1A​,μ1B​估计器下分别产生样本集合 s 1 ( A ) , s 1 ( B ) s_1^{(A)},s_1^{(B)} s1(A)​,s1(B)​的期望结果均已求解完毕。那么整个随机变量集合 X = { x 1 , x 2 , ⋯   , x M } \mathcal X=\{x_1,x_2,\cdots,x_M\} X={x1​,x2​,⋯,xM​}对应的期望结果表示如下： μ i A ( S ) ( i = 1 , 2 , . . . , M ) = { μ 1 A ( S ) , μ 2 A ( S ) , ⋯   , μ M A ( S ) } μ i B ( S ) ( i = 1 , 2 , . . . , M ) = { μ 1 B ( S ) , μ 2 B ( S ) , ⋯   , μ M B ( S ) } \mu_i^A(S)(i=1,2,...,M) = \{\mu_1^A(S),\mu_2^A(S),\cdots,\mu_M^A(S)\} \\ \mu_i^B(S)(i=1,2,...,M) = \{\mu_1^B(S),\mu_2^B(S),\cdots,\mu_M^B(S)\} μiA​(S)(i=1,2,...,M)={μ1A​(S),μ2A​(S),⋯,μMA​(S)}μiB​(S)(i=1,2,...,M)={μ1B​(S),μ2B​(S),⋯,μMB​(S)}

定义一个新的概念： M a x A ( S ) Max^A(S) MaxA(S)，它表示：选择 μ i A ( S ) \mu_i^A(S) μiA​(S)集合中数值最大结果对应随机变量下标的集合，数学符号表示如下： 在真实环境中，数值最大的结果可能不止一个，可能存在不同下标对应结果相等且均为最大值的情况出现。 M a x A ( S ) = { j ∣ μ j A ( S )   = max ⁡ i μ i A ( S ) } ( j ∈ 1 , 2 , ⋯   , M ) Max^A(S) = \{j \mid \mu_j^A(S)\ = \mathop{\max}\limits_{i} \mu_i^A(S)\}(j \in 1,2,\cdots,M) MaxA(S)={j∣μjA​(S) =imax​μiA​(S)}(j∈1,2,⋯,M) 需要注意的点：

• M a x A ( S ) Max^A(S) MaxA(S)集合中的元素可能存在若干个；
• 它存储的是结果对应的随机变量下标，而不是结果本身；

同理， M a x B ( S ) Max^B(S) MaxB(S)表示如下： M a x B ( S ) = { j ∣ μ j B ( S )   = max ⁡ i μ i B ( S ) } ( j ∈ 1 , 2 , ⋯   , M ) Max^B(S) = \{j \mid \mu_j^B(S)\ = \mathop{\max}\limits_{i} \mu_i^B(S)\}(j \in 1,2,\cdots,M) MaxB(S)={j∣μjB​(S) =imax​μiB​(S)}(j∈1,2,⋯,M)

核心思路 由于 μ A , μ B \mu^A,\mu^B μA,μB两个估计器都是对随机变量集合 X \mathcal X X进行采样，并且采集的样本相互独立。因此理论上，无论哪个估计器对 X \mathcal X X进行采样，它们都是对随机变量 X \mathcal X X的期望进行无偏估计： E [ μ i A ] = E [ μ i B ] = E [ x i ] ( i = 1 , 2 , ⋯   , M ) \mathbb E[\mu_i^A] = \mathbb E[\mu_i^B] = \mathbb E[x_i](i = 1,2,\cdots,M) E[μiA​]=E[μiB​]=E[xi​](i=1,2,⋯,M)

换句话说： 理论上，通过估计器 μ i A , μ i B \mu_i^A,\mu_i^B μiA​,μiB​分别对随机变量 x i x_i xi​采集的样本 s i ( A ) , s i ( B ) s_i^{(A)},s_i^{(B)} si(A)​,si(B)​的分布是相同的。

因此(双估计器的核心思想)：理论上， M a x A ( S ) Max^A(S) MaxA(S)中得到的随机变量下标的集合同样与 M a x B ( S ) Max^B(S) MaxB(S)中的下标集合是 可以共用的。 从理想状况下考虑，两者得到的下标集合甚至可能是‘高度重合的’。

基于上述思路，处理方法如下：

• 从 M a x A ( s ) Max^A(s) MaxA(s)下标集合中随机选择一个随机变量下标元素，命名为 a ∗ a^* a∗。那么 a ∗ a^* a∗一定满足： μ a ∗ A ( S ) = max ⁡ i μ i A ( S ) = max ⁡ i E { μ i A } ≈ max ⁡ i E [ x i ] \mu_{a^*}^A(S) = \mathop{\max}\limits_{i}\mu_i^A(S) = \mathop{\max}\limits_{i}\mathbb E\{\mu_i^{A}\} \approx \mathop{\max}\limits_{i} \mathbb E[x_i] μa∗A​(S)=imax​μiA​(S)=imax​E{μiA​}≈imax​E[xi​]
• 根据 双估计器方法的核心思想，估计器 μ B \mu^B μB对应 a ∗ a^* a∗位置的期望结果 μ a ∗ B ( S ) \mu_{a^*}^B(S) μa∗B​(S)同样可以用来近似估计随机变量 x i x_i xi​的期望 E [ x i ] \mathbb E[x_i] E[xi​]： μ a ∗ B ( S ) = max ⁡ i μ i B ( S ) = max ⁡ i E { μ i B } ≈ max ⁡ i E [ x i ] \mu_{a^*}^B(S) = \mathop{\max}\limits_{i}\mu_i^B(S) = \mathop{\max}\limits_{i}\mathbb E\{\mu_i^{B}\}\approx \mathop{\max}\limits_{i} \mathbb E[x_i] μa∗B​(S)=imax​μiB​(S)=imax​E{μiB​}≈imax​E[xi​]
• 在 极限情况 下(在采样数量足够多的情况下)，估计器 μ i A ， μ i B \mu_i^A，\mu_i^B μiA​，μiB​采集的数据集 s i ( A ) , s i ( B ) s_i^{(A)},s_i^{(B)} si(A)​,si(B)​的分布是无限接近的。从而有： μ i A ( S ) = μ i B ( S ) = E [ x i ] \mu_i^A(S) = \mu_i^B(S) = \mathbb E[x_i] μiA​(S)=μiB​(S)=E[xi​]

Double Q-Learning方法

在介绍完双估计器方法后，Double Q-Learning方法显得明朗了许多。观察如何将双估计器方法的思想应用在 时序差分方法 中。

时序差分方法的主要特点是：每次迭代只更新 Q − T a b l e Q-Table Q−Table中的某一个位置的元素—— Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)。即便一次只更新一个样本，仍然可以使用动量更新方式求解期望结果。 具体算法过程如下所示： 与双估计器方法主要流程对比如下：

• 初始化两个相互独立的 Q − T a b l e → Q A , Q B Q-Table \to Q^A,Q^B Q−Table→QA,QB，可以将 Q A , Q B Q^A,Q^B QA,QB想象成各自通过估计器产生的样本集合；

• 根据 双估计器方法的核心思想，将具体动作看作双估计器方法中的随机变量下标，以 Q A Q^A QA为例， S t + 1 S_{t+1} St+1​状态下，从 Q A Q^A QA中 选取最优动作集合 M a x A ( Q ( S t + 1 ) ) Max^A(Q(S_{t+1})) MaxA(Q(St+1​))表示如下： 同上，在真实环境中，可能存在不同动作对应的状态-动作价值函数结果相同且均为最大值的情况出现。 M a x A ( Q ( S t + 1 ) ) = { a ′ ∣   Q A ( S t + 1 , a ′ ) = max ⁡ a Q A ( S t + 1 , a ) } ( a ∈ A ( S t + 1 ) ) Max^A(Q(S_{t+1})) = \{a ' \mid \ Q^A(S_{t+1},a')= \mathop{\max}\limits_{a}Q^A(S_{t+1},a)\}(a \in \mathcal A(S_{t+1})) MaxA(Q(St+1​))={a′∣ QA(St+1​,a′)=amax​QA(St+1​,a)}(a∈A(St+1​))

• 从 最优动作集合 中任意选取一个动作 a ∗ a^* a∗，并将该动作对应在 Q B Q^B QB位置的元素 Q B ( S t + 1 , a ∗ ) Q^B(S_{t+1},a^*) QB(St+1​,a∗)取出，对 Q A Q^A QA执行增量更新过程： Q A ( S t , A t ) ← Q A ( S t , A t ) + α ( R t + 1 + γ Q B ( S t + 1 , a ∗ ) − Q A ( S t , A t ) ) Q^A(S_t,A_t) \gets Q^A(S_t,A_t) + \alpha(R_{t+1} + \gamma Q^B(S_{t+1},a^*) - Q^A(S_t,A_t)) QA(St​,At​)←QA(St​,At​)+α(Rt+1​+γQB(St+1​,a∗)−QA(St​,At​))

  同理， Q B Q^B QB的更新操作和 Q A Q^A QA相同； M a x B ( Q ( S t + 1 ) ) = { a ′ ∣   Q B ( S t + 1 , a ′ ) = max ⁡ a Q B ( S t + 1 , a ) } ( a ∈ A ( S t + 1 ) ) Q B ( S t , A t ) ← Q B ( S t , A t ) + α ( R t + 1 + γ Q A ( S t + 1 , a ∗ ) − Q B ( S t , A t ) ) Max^B(Q(S_{t+1})) = \{a ' \mid \ Q^B(S_{t+1},a')= \mathop{\max}\limits_{a}Q^B(S_{t+1},a)\}(a \in \mathcal A(S_{t+1})) \\ Q^B(S_t,A_t) \gets Q^B(S_t,A_t) + \alpha(R_{t+1} + \gamma Q^A(S_{t+1},a^*) - Q^B(S_t,A_t)) MaxB(Q(St+1​))={a′∣ QB(St+1​,a′)=amax​QB(St+1​,a)}(a∈A(St+1​))QB(St​,At​)←QB(St​,At​)+α(Rt+1​+γQA(St+1​,a∗)−QB(St​,At​))

• 每一次迭代过程只会更新一个 Q − T a b l e Q-Table Q−Table，为了使 Q A , Q B Q^A,Q^B QA,QB分布 尽可能相似 → Q A , Q B \to Q^A,Q^B →QA,QB被选中的概率相等，通常处理方式是通过从0-1均匀分布中随机选取一值，观察该值和0.5的大小关系。这种方法有： P ( Q u s e A ) = P ( Q u s e B ) = 0.5 P(Q_{use}^A) = P(Q_{use}^B) = 0.5 P(QuseA​)=P(QuseB​)=0.5

至此，使用双估计器方法解读Double Q-Learning方法结束。

Double Q-Learning方法中的一个细节

在上述算法描述中，结合双估计器方法的核心思想， Q A , Q B Q^A,Q^B QA,QB两个 Q − T a b l e Q-Table Q−Table内部分布是高度相似的。 但在算法初始——使用 ϵ − \epsilon- ϵ−贪心策略选择 t t t时刻的动作 A t A_t At​ 过程中，使用的 Q − T a b l e Q-Table Q−Table将 Q A , Q B Q^A,Q^B QA,QB两个结果对应元素相加结果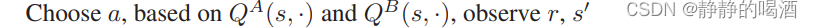： 理论上，两个期望高度相似的 Q − T a b l e Q-Table Q−Table相加 并不影响分布的变化，为什么要执行这种操作？执行如下实验： 最后附Double Q-Learning的完整代码

• ϵ − \epsilon- ϵ−贪心策略部分使用 Q A , Q B Q^A,Q^B QA,QB结果对应元素相加操作；
• ϵ − \epsilon- ϵ−贪心策略部分直接使用 Q A , Q B Q^A,Q^B QA,QB中的任意一个；

这里仍然使用最大化偏差问题与Double Q-Learning(一)——最大化偏差问题介绍中的示例环境，返回结果如下图所示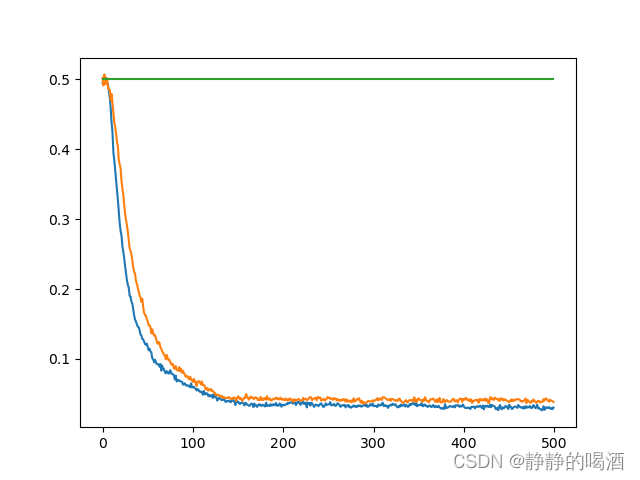： 其中，蓝色线 表示“ Q − T a b l e Q-Table Q−Table对应元素相加”操作；黄色线 表示“选择任意 Q − T a b l e Q-Table Q−Table”操作，明显能够观察到：蓝色线的斜率比黄色线更“陡”——蓝色线操作让模型能够更快地选择正确的方向。 从理论角度思考，这种对应元素相加操作可以看成 将两个估计器 μ A , μ B \mu^A,\mu^B μA,μB采集到的样本放在了一起——增加了集合中样本的数量，估计结果自然更加准确了。

附：Double Q-Learning方法完整代码示例

import numpy as np
import random
from tqdm import trange


class Env():
    '''构造一个环境类'''

    def __init__(self, mu, sigma, nB):
        self.mu = mu
        self.sigma = sigma
        self.STATE_A = self.left = 0
        self.STATE_B = self.right = 1
        self.Terminal = 2
        self.nS = 3  # 加上Terminal即3个状态
        self.nA = 2
        self.nB = nB  # 状态B的动作数
        self.state = self.STATE_A

    def reset(self):
        self.state = self.STATE_A
        return self.state

    def step(self, action):
        # A--left
        if self.state == self.STATE_A and action == self.left:
            self.state = self.STATE_B
            return self.state, 0, False  # next_state, reward, done
        # A--right
        elif self.state == self.STATE_A and action == self.right:
            self.state = self.Terminal
            return self.state, 0, True
        # B--all_actions
        elif self.state == self.STATE_B:
            self.state = self.Terminal
            reward = random.normalvariate(self.mu, self.sigma)
            return self.state, reward, True

def init_Q_table(env):
    '''初始化Q表'''
    Q = {env.STATE_A:{action:0 for action in range(env.nA)},
         env.STATE_B:{action:0 for action in range(env.nB)},
         env.Terminal:{action:0 for action in range(env.nA)}}
    return Q

def select_action_behavior_policy(action_value_dict, epsilon):
    '''使用epsilon-greedy采样action'''
    if random.random() > epsilon:
        max_keys = [key for key, value in action_value_dict.items() if value == max( action_value_dict.values() )]
        action = random.choice(max_keys)
    else:
        # 从Q字典对应state中随机选取1个动作,由于返回list,因此通过[0]获取元素
        action = random.sample(action_value_dict.keys(), 1)[0]
    return action


def get_Q1_add_Q2(Q1_state_dict, Q2_state_dict):
    '''
    返回Q1[state]+Q2[state]
    '''
    return {action: Q1_value + Q2_state_dict[action] for action, Q1_value in Q1_state_dict.items()}

def double_Q_learning(env, alpha=0.2, epsilon_scope=[0.2,0.05,0.99], num_of_episode=1000, gamma=0.9,add_opera=True):
    '''
    双Q学习算法; 其中epsilon_scope由高到低衰减,从左到右分别是[最高值,最低值,衰减因子]
    '''
    epsilon = epsilon_scope[0]
    select_l = []
    # 1. 初始化Q1表和Q2表
    Q1 = init_Q_table(env)
    Q2 = init_Q_table(env)

    for num in range(num_of_episode):
        state = env.reset()  # Init S
        count = 0
        while True:
            count += 1
            # 2.通过behavior policy采样action
            if add_opera:
                add_Q1_Q2_state = get_Q1_add_Q2(Q1[state], Q2[state])
            else:
                add_Q1_Q2_state = Q1[state]
            action = select_action_behavior_policy(add_Q1_Q2_state, epsilon)
            # 3.执行action并观察R和next state
            next_state, reward, done = env.step(action)
            # 4.更新Q(S,A),使用max操作更新
            if random.random() >= 0.5:
                # 从Q1表中的下一步state找出状态价值最高对应的action视为Q1[state]的最优动作
                A1 = random.choice( [action for action, value in Q1[next_state].items() if value == max( Q1[next_state].values() )] )
                # 将Q1[state]得到的最优动作A1代入到Q2[state][A1]中的值作为Q1[state]的更新
                Q1[state][action] += alpha * (reward + gamma*Q2[next_state][A1] - Q1[state][action])
            else:
                A2 = random.choice( [action for action, value in Q2[next_state].items() if value == max( Q2[next_state].values() )] )
                Q2[state][action] += alpha * (reward + gamma*Q1[next_state][A2] - Q2[state][action])
            if done: break
            state = next_state
        if count > 1:
            select_l.append(1)
        else:
            select_l.append(0)
        # 对epsilon进行衰减
        if epsilon >= epsilon_scope[1]: epsilon *= epsilon_scope[2]
    return Q1,select_l

if __name__ == '__main__':
    env = Env(-0.1, 1, 10)
    # Double Q-learning学习出Q1≈Q2表

    stat_double_q_learning = []
    stat_double_q_learning_singleQ = []

    for i in trange(10000):
        _, select_l = double_Q_learning(env, alpha=0.2, epsilon_scope=[0.2, 0.05, 0.99], num_of_episode=500, gamma=0.9)
        _, select_l_singleQ = double_Q_learning(env, alpha=0.2, epsilon_scope=[0.2, 0.05, 0.99], num_of_episode=500,
                                                gamma=0.9, add_opera=False)

        stat_double_q_learning.append(select_l)
        stat_double_q_learning_singleQ.append(select_l_singleQ)

    import matplotlib.pyplot as plt

    k_double = np.array(stat_double_q_learning)
    k_double_singleQ = np.array(stat_double_q_learning_singleQ)

    x = [i for i in range(500)]
    plt.plot(x, np.mean(k_double, axis=0))
    plt.plot(x, np.mean(k_double_singleQ, axis=0))

    plt.plot(x, [0.5 for _ in x])
    plt.show()

至此，关于Double Q-Learning方法的介绍全部结束，下一节将介绍策略梯度方法求解强化学习系列。

相关参考： 深度强化学习系列(5): Double Q-Learning原理详解 解剖[强化学习]Double Learning本质并对比Q-Learning与期望Sarsa