机器学习笔记之指数族分布——最大熵角度观察指数族分布(一)最大熵思想

引言

上一节介绍了指数族分布的通式以及共轭性质，本节将通过代码示例共轭性质，并介绍最大熵思想。

补充：指数族分布的共轭性质

指数族分布的共轭性质主要面对贝叶斯估计中分母积分难的问题： P ( θ ∣ x ) = P ( x ∣ θ ) ⋅ P ( θ ) ∫ θ P ( x ∣ θ ) ⋅ P ( θ ) d θ \mathcal P(\theta \mid x) = \frac{\mathcal P(x \mid \theta) \cdot \mathcal P(\theta)}{\int_{\theta} \mathcal P(x \mid \theta) \cdot \mathcal P(\theta)d\theta} P(θ∣x)=∫θ​P(x∣θ)⋅P(θ)dθP(x∣θ)⋅P(θ)​

因此，共轭性质的具体表述逻辑如下：

• 如果概率模型(似然函数) P ( x ∣ θ ) \mathcal P(x \mid \theta) P(x∣θ)分布 存在一个共轭的先验分布 P ( θ ) \mathcal P(\theta) P(θ)，那么效果是：后验分布 P ( θ ∣ x ) \mathcal P(\theta \mid x) P(θ∣x)与先验分布 P ( θ ) \mathcal P(\theta) P(θ)会形成相同分布形式。 P ( θ ∣ x ) ∝ P ( x ∣ θ ) ⋅ P ( θ ) \mathcal P(\theta \mid x) \propto \mathcal P(x \mid \theta) \cdot \mathcal P(\theta) P(θ∣x)∝P(x∣θ)⋅P(θ)

示例： 假设似然概率是二项式分布，关于似然概率 P ( x ∣ θ ) \mathcal P(x \mid \theta) P(x∣θ)中的参数 θ \theta θ的概率 P ( θ ) \mathcal P(\theta) P(θ)服从 Beta \text{Beta} Beta分布，那么后验概率的分布 P ( θ ∣ x ) \mathcal P(\theta \mid x) P(θ∣x)同样也服从 Beta \text{Beta} Beta分布，但该分布与 P ( θ ) \mathcal P(\theta) P(θ)服从的 Beta \text{Beta} Beta分布不一定相同。 具体代码如下： 首先构建一个二项分布的随机数，执行120次试验，并将试验结果归一化为 ( 0 , 1 ) (0,1) (0,1)范围内的结果：

import nunmpy as np

def get_Binormal():
    outcome = np.random.binomial(13001,0.5,120)
    # outcome = np.random.binormal(13001,0.5,12000)
    max_out = max(outcome)
    return [(i / max_out) for i in outcome]

返回结果如下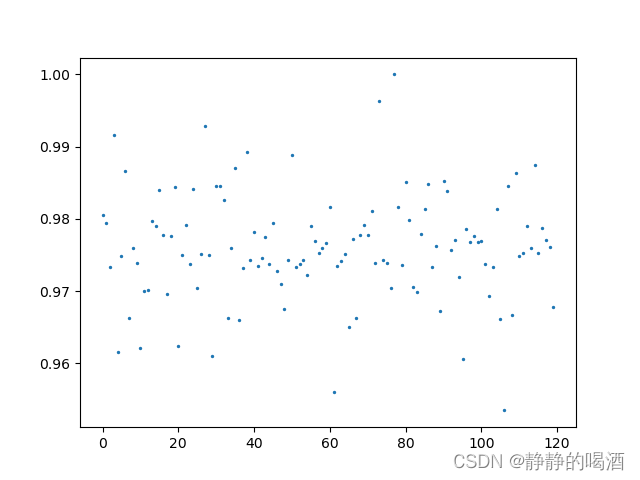： 可能只能看出一点规律，如果将试验次数增加至12000次，再次观察分布结果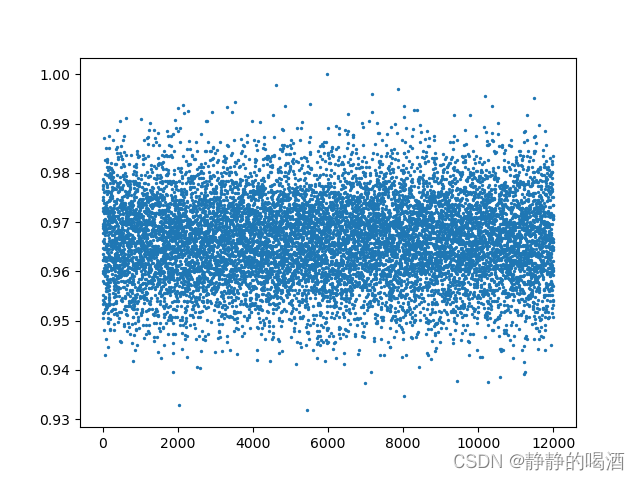： 此时发现，这明显是高斯分布的随机点图像。当观测序列足够大时，二项分布近似于高斯分布传送门。回归正题，接下来构建一个关于 Beta \text{Beta} Beta分布的随机数：

from scipy.stats import beta

def get_beta(a,b,sample_num):
    x = np.linspace(0,1,sample_num)
    return beta.pdf(x,a,b)
    
out = get_beta(1.4,1.2,120)

返回随机数图像结果如下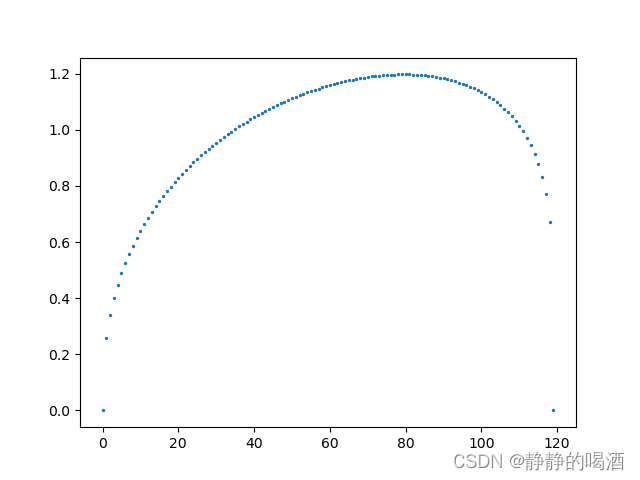： 最后将两组随机数对应元素做乘法，观察结果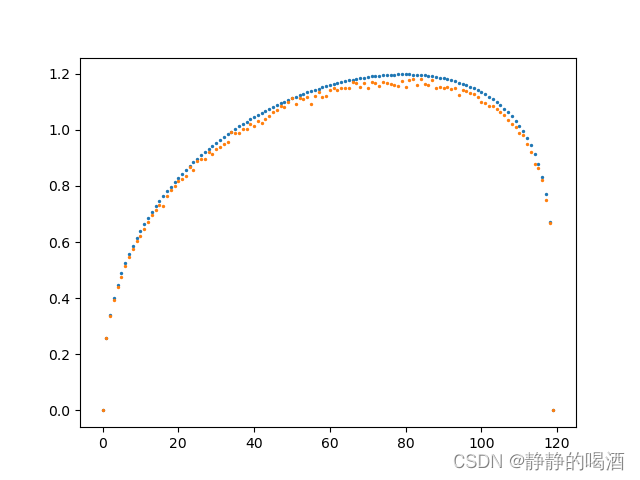： 如果两种分布采样次数越多，其乘法分布结果就越稳定。下面是采样2000次时的结果图像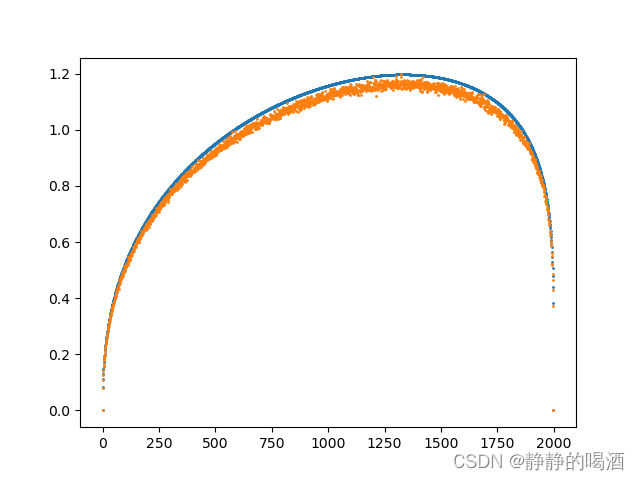： 完整代码如下：

from scipy.stats import beta
import numpy as np

import matplotlib.pyplot as plt

def get_Binormal(rate):
    outcome = np.random.binomial(13001,rate,200)
    max_out = max(outcome)
    return [(i / max_out) for i in outcome]

def get_beta(a,b,sample_num):
    x = np.linspace(0,1,sample_num)
    return beta.pdf(x,a,b)

if __name__ == '__main__':
    out = get_beta(1.4,1.2,200)
    x = [i for i in range(len(out))]
    bi_out = get_Binormal(rate=0.01)
    bi_out_ = get_Binormal(rate=0.99)

    final_out = out * bi_out
    final_out_ = out * bi_out_

    plt.scatter(x,out,s=1)
    plt.scatter(x,final_out,s=1)
    plt.scatter(x,final_out_,s=1)
    plt.show()

最大熵思想介绍 信息量

信息本身就伴随着 不确定性(或者说信息自身存在随机性)。而信息量大小表示信息消除不确定性的程度。

• 如果某个事件发生的概率 p = 1 p=1 p=1恒成立，例如：太阳从东方升起。这条信息的不确定性为 0 0 0，自然不存在消除不确定性的说法。 从该例子中发现，至少要存在不确定性，才有机会谈到不确定性消除的概念。
• 另一个例子：我中了5000万。由于中奖的概率极低，假设是99.9%(当然实际上比该数值还要低)，那么这条信息就 排除 了99.9%概率的事件——我没有中5000万，这可以看出这条信息消除不确定性的程度很高。

从上述两个例子可以发现，信息消除不确定性的程度和信息本身发生的概率成反比关系。

信息量的公式表示如下： h ( x ) = log ⁡ 1 p ( x ) = − log ⁡ p ( x ) h(x) = \log \frac{1}{p(x)} = -\log p(x) h(x)=logp(x)1​=−logp(x) 其中， h ( x ) h(x) h(x)表示事件 x x x的信息量，而 p ( x ) p(x) p(x)表示事件 x x x发生的概率。将上述两个例子带入到上式中：

• x 1 → x_1\to x1​→{“太阳从东方升起”}， p ( x 1 ) = 1 , h ( x 1 ) = log ⁡ 1 1 = 0 p(x_1)=1,h(x_1) = \log \begin{aligned}\frac{1}{1}\end{aligned} = 0 p(x1​)=1,h(x1​)=log11​​=0；
• x 2 → x_2 \to x2​→{“我中了5000万”}， p ( x 2 ) = 0.001 , h ( x 2 ) = log ⁡ 1 0.001 ≈ 6.907 p(x_2)=0.001,h(x_2) = \log \frac{1}{0.001} \approx 6.907 p(x2​)=0.001,h(x2​)=log0.0011​≈6.907

该公式完全符合上述逻辑关系。

熵 ( Entropy ) (\text{Entropy}) (Entropy)

从信息量的角度，熵是事件的信息量在事件发生概率分布下的期望。记事件 x x x的熵为 H ( x ) \mathcal H(x) H(x)，其具体表示方法如下： H ( x ) = E p ( x ) [ h ( x ) ] = E p ( x ) [ log ⁡ 1 p ( x ) ] \begin{aligned} \mathcal H(x) & = \mathbb E_{p(x)}\left[h(x)\right] \\ & = \mathbb E_{p(x)}\left[\log\frac{1}{p(x)}\right] \end{aligned} H(x)​=Ep(x)​[h(x)]=Ep(x)​[logp(x)1​]​

• 如果概率分布 p ( x ) p(x) p(x)是连续型随机变量， H ( x ) \mathcal H(x) H(x)可以表示为： H ( x ) = − ∫ x p ( x ) log ⁡ p ( x ) d x \mathcal H(x) =- \int_{x} p(x)\log p(x) dx H(x)=−∫x​p(x)logp(x)dx
• 如果概率分布 p ( x ) p(x) p(x)是离散型级变量， H ( x ) \mathcal H(x) H(x)可以表示为： H ( x ) = − ∑ x p ( x ) log ⁡ p ( x ) \mathcal H(x) = - \sum_{x} p(x) \log p(x) H(x)=−x∑​p(x)logp(x)
• 更细致的理解思路： 假设某数据集合 X \mathcal X X包含数量为 N N N的样本： X = { x ( 1 ) , x ( 2 ) , x ( 3 ) , ⋯   , x ( N ) } \mathcal X = \left\{x^{(1)},x^{(2)},x^{(3)},\cdots,x^{(N)} \right\} X={x(1),x(2),x(3),⋯,x(N)} 关于数据集合的熵 H ( X ) \mathcal H(\mathcal X) H(X)表示如下： H ( X ) = − ∑ i = 1 N p ( x ( i ) ) log ⁡ p ( x ( i ) ) \mathcal H(\mathcal X) = -\sum_{i=1}^N p(x^{(i)})\log p(x^{(i)}) H(X)=−i=1∑N​p(x(i))logp(x(i))

最大熵思想

从实际意义的角度，熵可以表示信息可能性的一种衡量，而最大熵思想具体意义是指：如果对某一数据集合 X \mathcal X X的概率模型 P ( x ∣ θ ) P(x \mid \theta) P(x∣θ)未知的情况下：

• 在概率模型学习的过程中，熵最大的模型是最优模型；如果概率模型 P ( x ∣ θ ) P(x\mid \theta) P(x∣θ)存在约束条件，则满足约束条件下熵最大的模型是最优模型。

最大熵思想的核心：等可能。 什么叫等可能？这是最大熵的理想状态：希望概率模型中各样本以相同概率的形式出现，此时的熵最大。 但是概率分布 我们说的不算，它是概率模型自身性质产生的。换个思路，概率模型的概率分布是客观存在的，不受人的意志变化而变化。因此，最大熵的出现为另外一种思路提供了一种有效工具：

虽然不能改变概率分布自身，但我们总希望这个概率分布能够涵盖到更多数量的样本，这种概率分布能够更加泛化、更大程度地对概率模型中所有样本通用。

至此，我们继续观察基于数据集合 X \mathcal X X熵的公式，将公式展开： H ( X ) = ∑ i = 1 N p ( x ( i ) ) log ⁡ 1 p ( x ( i ) ) = p ( x ( 1 ) ) log ⁡ 1 p ( x ( 1 ) ) + p ( x ( 2 ) ) log ⁡ 1 p ( x ( 2 ) ) + ⋯ + p ( x ( N ) ) log ⁡ 1 p ( x ( N ) ) \begin{aligned} \mathcal H(\mathcal X) & = \sum_{i=1}^N p(x^{(i)})\log \frac{1}{p(x^{(i)})} \\ & = p(x^{(1)})\log \frac{1}{p(x^{(1)})} + p(x^{(2)})\log \frac{1}{p(x^{(2)})} + \cdots +p(x^{(N)})\log \frac{1}{p(x^{(N)})} \end{aligned} H(X)​=i=1∑N​p(x(i))logp(x(i))1​=p(x(1))logp(x(1))1​+p(x(2))logp(x(2))1​+⋯+p(x(N))logp(x(N))1​​

观察任意一项，发现概率 p ( x ( i ) ) p(x^{(i)}) p(x(i))与 log ⁡ 1 p ( x ( i ) ) \begin{aligned}\log \frac{1}{p(x^{(i)})}\end{aligned} logp(x(i))1​​之间的 单调性完全相反：我们画出 p log ⁡ 1 p \begin{aligned}p \log\frac{1}{p}\end{aligned} plogp1​​在 p ∈ ( 0 , 1 ) p \in(0,1) p∈(0,1)范围内的图像如下： 通过观察发现，即便不知道概率模型的概率分布，但是熵的每一项取值是有界的(单个项的最优解不超过 0.4 0.4 0.4)。因此，用通俗的话说，想通过聚焦个别样本预测概率分布使熵达到最大是行不通的。 这种预测方式的熵反而很小——仅照顾到个别样本，而更多的样本的熵值被放弃掉了，预测的概率分布结果自然是很局限的，不能代表所有样本。

因此，更一般的思想是希望预测的概率分布尽可能照顾到更多样本，高的不要太高，低的不要太低，对应的 p ( x ) log ⁡ 1 p ( x ) \begin{aligned}p(x) \log \frac{1}{p(x)}\end{aligned} p(x)logp(x)1​​在各样本间差距尽量的小，从而使每个样本结果都有一个比较不错的熵值，从而使熵达到最大。

综上，最大熵的目的是尽可能的抹除各样本间被选择概率的区别性。

最大熵思想示例

目标：如果对数据集合 X \mathcal X X的概率模型 P ( x ∣ θ ) \mathcal P(x \mid \theta) P(x∣θ)未知的情况下，观察 什么类型的概率分布使熵达到最大；

准备工作：

• 假设样本集合 X \mathcal X X中样本 x x x是离散型随机变量；
• 定义样本 x x x的概率分布： 由于是离散型随机变量，这里使用1，2，3...表示选择的离散信息,即维度; 并满足： ∑ i = 1 k p i ( x ) = 1 \sum_{i=1}^k p_i(x) = 1 i=1∑k​pi​(x)=1

x x x12… k k k p p p p 1 ( x ) p_1(x) p1​(x) p 2 ( x ) p_2(x) p2​(x)… p k ( x ) p_k(x) pk​(x)

推导过程： 上述问题可看作优化问题：

• 优化函数： max ⁡ H [ P ( x ) ] = max ⁡ − ∑ i = 1 k p i ( x ) log ⁡ p i ( x ) \begin{aligned}\max \mathcal H[\mathcal P(x)] = \max - \sum_{i=1}^k p_i(x) \log p_i(x)\end{aligned} maxH[P(x)]=max−i=1∑k​pi​(x)logpi​(x)​
• 条件： ∑ i = 1 k p i ( x ) = 1 \begin{aligned}\sum_{i=1}^k p_i(x) = 1\end{aligned} i=1∑k​pi​(x)=1​

整理： { max ⁡ H [ P ( x ) ] = max ⁡ − ∑ i = 1 k p i ( x ) log ⁡ p i ( x ) = min ⁡ ∑ i = 1 k p i ( x ) log ⁡ p i ( x ) s . t . ∑ i = 1 k p i ( x ) = 1 \begin{cases} \begin{aligned} \max \mathcal H[P(x)] & = \max - \sum_{i=1}^k p_i(x) \log p_i(x) \\ & = \min \sum_{i=1}^k p_i(x) \log p_i(x) \\ s.t.\quad\sum_{i=1}^k p_i(x) & = 1 \end{aligned} \end{cases} ⎩ ⎨ ⎧​maxH[P(x)]s.t.i=1∑k​pi​(x)​=max−i=1∑k​pi​(x)logpi​(x)=mini=1∑k​pi​(x)logpi​(x)=1​​ 令 P ( x ) \mathcal P(x) P(x)为表示概率分布向量： P ( x ) = [ p 1 ( x ) p 2 ( x ) ⋮ p k ( x ) ] k × 1 \mathcal P(x) = \begin{bmatrix} p_1(x) \\ p_2(x) \\ \vdots \\ p_k(x) \end{bmatrix}_{k \times 1} P(x)= ​p1​(x)p2​(x)⋮pk​(x)​ ​k×1​

目标是求解 k k k个最优概率分布，使得熵 H [ P ( x ) ] \mathcal H[P(x)] H[P(x)]最大。 p ^ i ( x ) = arg ⁡ max ⁡ p i ( x ) H [ P ( x ) ] = arg ⁡ min ⁡ p i ( x ) ∑ i = 1 k p i ( x ) log ⁡ p i ( x ) i = 1 , 2 , ⋯   , k \begin{aligned} \hat p_i (x) & = \mathop{\arg\max}\limits_{p_i(x)} \mathcal H[P(x)] \\ & = \mathop{\arg\min}\limits_{p_i(x)} \sum_{i=1}^kp_i(x) \log p_i(x) \quad i = 1,2,\cdots,k \end{aligned} p^​i​(x)​=pi​(x)argmax​H[P(x)]=pi​(x)argmin​i=1∑k​pi​(x)logpi​(x)i=1,2,⋯,k​ 该式理解为：分别取到 p ^ 1 ( x ) , p ^ 2 ( x ) , . . . , p ^ k ( x ) \hat p_1(x),\hat p_2(x),...,\hat p_k(x) p^​1​(x),p^​2​(x),...,p^​k​(x),构成 ( p ^ 1 ( x ) p ^ 2 ( x ) ⋮ p ^ k ( x ) ) \begin{pmatrix} \hat p_1(x) \\ \hat p_2(x) \\ \vdots \\ \hat p_k(x) \end{pmatrix} ​p^​1​(x)p^​2​(x)⋮p^​k​(x)​ ​使得 H [ P ( x ) ] \mathcal H[P(x)] H[P(x)]最大。 上述描述是 带一个约束，并且是等号约束的优化问题，因此，使用拉格朗日乘数法进行求解。

• 定义拉格朗日函数： L [ P ( x ) , λ ] = ∑ i = 1 k p i ( x ) log ⁡ p i ( x ) + λ [ 1 − ∑ i = 1 k p i ( x ) ] \mathcal L[P(x),\lambda] = \sum_{i=1}^k p_i(x) \log p_i(x) + \lambda \left[1 - \sum_{i=1}^k p_i(x) \right] L[P(x),λ]=i=1∑k​pi​(x)logpi​(x)+λ[1−i=1∑k​pi​(x)]
• 拉格朗日函数 L [ P ( x ) , λ ] \mathcal L[P(x),\lambda] L[P(x),λ]对每一维度的概率分布 p i ( x ) i = 1 , 2 , ⋯   , k p_i(x)\quad i=1,2,\cdots,k pi​(x)i=1,2,⋯,k求偏导： 由于只对 p i ( x ) p_i(x) pi​(x)求解偏导，因此 p 1 ( x ) , p 2 ( x ) , ⋯   , p i − 1 ( x ) , p i + 1 ( x ) , ⋯   , p k ( x ) p_1(x),p_2(x),\cdots,p_{i-1}(x),p_{i+1}(x),\cdots,p_k(x) p1​(x),p2​(x),⋯,pi−1​(x),pi+1​(x),⋯,pk​(x)都是常数。 ∂ L ∂ p i ( x ) = log ⁡ p i ( x ) + p i ( x ) ⋅ 1 p i ( x ) − λ = log ⁡ p i ( x ) + 1 − λ \begin{aligned} \frac{\partial \mathcal L}{\partial p_i(x)} & = \log p_i(x) + p_i(x) \cdot \frac{1}{p_i(x)} - \lambda \\ & = \log p_i(x) + 1 - \lambda \end{aligned} ∂pi​(x)∂L​​=logpi​(x)+pi​(x)⋅pi​(x)1​−λ=logpi​(x)+1−λ​
• 求极值解：令 ∂ L ∂ p i ( x ) ≜ 0 \begin{aligned}\frac{\partial \mathcal L}{\partial p_i(x)} \triangleq 0\end{aligned} ∂pi​(x)∂L​≜0​： log ⁡ p ^ i ( x ) + 1 − λ = 0 p ^ i ( x ) = exp ⁡ { λ − 1 } \log \hat p_i(x) + 1 - \lambda = 0 \\ \hat p_i(x) = \exp \{\lambda - 1\} logp^​i​(x)+1−λ=0p^​i​(x)=exp{λ−1}

由于 λ \lambda λ是拉格朗日系数，是常数；因此对其他 p − i ( x ) p_{-i}(x) p−i​(x)求导同样会得到该常数： 概率的最优解和概率分布下标(维度)之间没有任何关系。 p − i ( x ) p_{-i}(x) p−i​(x)表示除去 p i ( x ) p_i(x) pi​(x)的其他维度的概率分布 p ^ 1 ( x ) = p ^ 2 ( x ) = ⋯ = p ^ k ( x ) = exp ⁡ { λ − 1 } \hat p_1(x) = \hat p_2(x) = \cdots = \hat p_k(x) = \exp \{\lambda - 1\} p^​1​(x)=p^​2​(x)=⋯=p^​k​(x)=exp{λ−1} 又因为： ∑ i = 1 k p ^ i ( x ) = 1 \sum_{i=1}^k \hat p_i(x) = 1 i=1∑k​p^​i​(x)=1 因此： p ^ 1 ( x ) = p ^ 2 ( x ) = ⋯ = p ^ k ( x ) = 1 k \hat p_1(x) = \hat p_2(x) = \cdots = \hat p_k(x) = \frac{1}{k} p^​1​(x)=p^​2​(x)=⋯=p^​k​(x)=k1​ 即样本 x x x选择任意一个离散信息的概率是相同的，因此， P ( x ) P(x) P(x)是均匀分布。

至此，在概率未知的情况下——不清楚 p i ( x ) ( i = 1 , 2 , ⋯   , k ) p_i(x) (i=1,2,\cdots,k) pi​(x)(i=1,2,⋯,k)的具体结果是什么，我们求得均匀分布是熵最大的分布。验证了上面的等可能思想。

相关参考： 二项分布与正态分布的关系是怎样的？ 机器学习-白板推导系列(八)-指数族分布（Exponential Family Distribution）