- 引言
- 高斯混合模型介绍
- 示例介绍
- 从几何角度观察高斯混合模型
- 从混合模型的角度观察
- 概率混合模型的引出
- 从概率生成模型的角度观察高斯混合模型
上一系列介绍了EM算法，本节将介绍第一个基于EM算法求解的概率生成模型——高斯混合模型(Gaussian Mixture Model,GMM)。
高斯混合模型介绍 示例介绍首先观察一张关于样本集合
X
\mathcal X
X的分布图：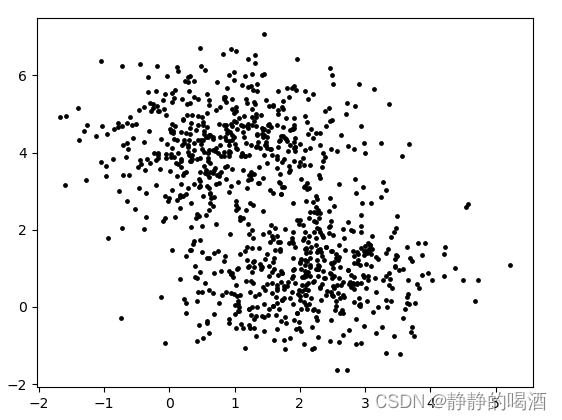 
从观察的视角对
X
\mathcal X
X的分布进行分析，感觉上述样本点明显存在两堆，当然也可以认为是一堆样本，可能是样本没有全部生成完而已。但从常理角度观察 更像是两种不同分布的样本点存在于同一个样本空间中。
我们假设上述两堆样本点每一堆均服从高斯分布，尝试对上述样本点横坐标的的概率密度函数(Probability Density Function,PDF)进行表示：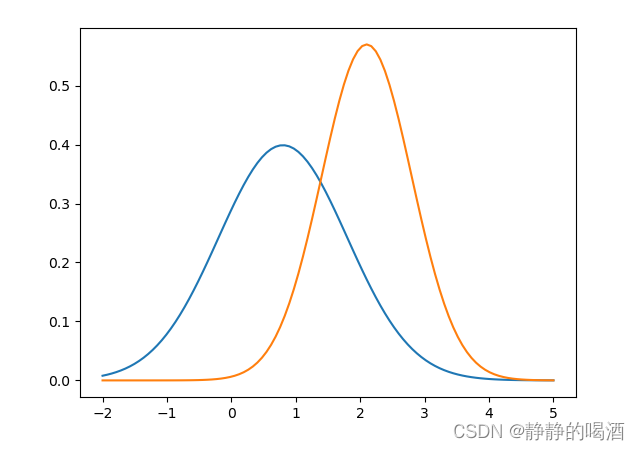 
该图意义是概率密度函数结果越高，该样本点存在更大的概率被产生出来。 观察上述所有样本点的横坐标，发现 以0.8和2.1这两个位置为中心，横坐标值围绕这两个中心产生的更密集，而其他位置相对稀疏一些。
因此，我们可以认为产生这些样本点的概率模型 P ( X ) P(\mathcal X) P(X)是由两个高斯分布混合在一起得到的混合模型。我们称这个概率模型 P ( X ) P(\mathcal X) P(X)为高斯混合模型。
从几何角度观察高斯混合模型
P
(
X
)
P(\mathcal X)
P(X)也自然存在概率密度函数。依然以上述样本点横坐标作为示例，它的概率密度函数大致表示如下：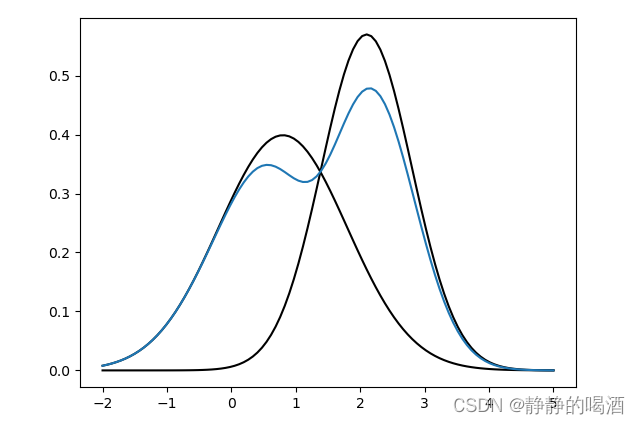 
其中这个蓝色线可看作概率分布
P
(
X
)
P(\mathcal X)
P(X)产生的样本横坐标的概率密度函数。以第
i
i
i个样本的横坐标
x
(
i
)
x^{(i)}
x(i)为例，它的具体计算方法如下：
x
m
i
x
(
i
)
=
f
1
(
x
(
i
)
)
f
1
(
x
(
i
)
)
+
f
2
(
x
(
i
)
)
⋅
f
1
(
x
(
i
)
)
+
[
1
−
f
1
(
x
(
i
)
)
f
1
(
x
(
i
)
)
+
f
2
(
x
(
i
)
)
]
⋅
f
2
(
x
(
i
)
)
=
[
f
1
(
x
(
i
)
)
]
2
+
[
f
(
x
(
i
)
)
]
2
f
1
(
x
(
i
)
)
+
f
2
(
x
(
i
)
)
\begin{aligned}x_{mix}^{(i)} & = \frac{f_1(x^{(i)})}{f_1(x^{(i)}) + f_2(x^{(i)})} \cdot f_1(x^{(i)}) + \left[1 - \frac{f_1(x^{(i)})}{f_1(x^{(i)}) + f_2(x^{(i)})}\right] \cdot f_2(x^{(i)}) \\ & = \frac{[f_1(x^{(i)})]^2 + [f_(x^{(i)})]^2}{f_1(x^{(i)}) + f_2(x^{(i)})} \end{aligned}
xmix(i)=f1(x(i))+f2(x(i))f1(x(i))⋅f1(x(i))+[1−f1(x(i))+f2(x(i))f1(x(i))]⋅f2(x(i))=f1(x(i))+f2(x(i))[f1(x(i))]2+[f(x(i))]2 其中，
f
1
,
f
2
f_1,f_2
f1,f2分别表示两种高斯分布的概率密度函数：
f
j
=
1
2
π
σ
j
e
−
(
x
i
−
μ
j
)
2
2
σ
j
2
(
j
=
1
,
2
)
f_j = \frac{1}{\sqrt{2\pi}\sigma_j}e^{-\frac{(x_i - \mu_j)^2}{2 \sigma_j^2}} \quad (j=1,2)
fj=2π
σj1e−2σj2(xi−μj)2(j=1,2) 我们可以将
x
m
i
x
(
i
)
x_{mix}^{(i)}
xmix(i)结果的生成看成两个步骤：
- 对应样本点横坐标 x ( i ) x^{(i)} x(i)，分别计算该样本点分别出现在分布1、分布2的比重 α 1 ( i ) , α 2 ( i ) \alpha_1^{(i)},\alpha_2^{(i)} α1(i),α2(i)： α 1 ( i ) = f 1 ( x ( i ) ) f 1 ( x ( i ) ) + f 2 ( x ( i ) ) , α 2 ( i ) = [ 1 − f 1 ( x ( i ) ) f 1 ( x ( i ) ) + f 2 ( x ( i ) ) ] \alpha_1^{(i)} = \frac{f_1(x^{(i)})}{f_1(x^{(i)}) + f_2(x^{(i)})} ,\alpha_2^{(i)} = \left[1 - \frac{f_1(x^{(i)})}{f_1(x^{(i)}) + f_2(x^{(i)})} \right] α1(i)=f1(x(i))+f2(x(i))f1(x(i)),α2(i)=[1−f1(x(i))+f2(x(i))f1(x(i))]
- 融合模型的概率密度结果表示为属于各分布的加权平均： x m i x ( i ) = α 1 ( i ) f 1 ( x ( i ) ) + α 2 ( i ) f 2 ( x ( i ) ) x_{mix}^{(i)} = \alpha_1^{(i)}f_1{(x^{(i)})} + \alpha_2^{(i)}f_2{(x^{(i)})} xmix(i)=α1(i)f1(x(i))+α2(i)f2(x(i))
因此，从图像角度观察可以将高斯混合模型理解为：样本空间中的任一维度均由多个高斯分布叠加而成，并且该模型的概率密度函数可表示为多个高斯分布的加权平均。
假设某高斯混合模型由 K \mathcal K K个高斯分布叠加而成，那么该模型的概率密度函数表示如下： P ( X ) = ∑ k = 1 K α k ⋅ N ( μ k , Σ k ) ( ∑ k = 1 K α k = 1 ) P(\mathcal X) = \sum_{k=1}^{\mathcal K} \alpha_{k} \cdot \mathcal N(\mu_{k},\Sigma_{k}) \quad (\sum_{k=1}^{\mathcal K} \alpha_k = 1) P(X)=k=1∑Kαk⋅N(μk,Σk)(k=1∑Kαk=1)
从混合模型的角度观察重新观察样本分布图，先设定数据集合中样本点的表示如下：
D
a
t
a
=
{
(
x
(
i
)
,
y
(
i
)
)
∣
i
=
1
N
}
Data = \left\{(x^{(i)},y^{(i)}) |_{i=1}^N\right\}
Data={(x(i),y(i))∣i=1N} 其中
x
(
i
)
,
y
(
i
)
x^{(i)},y^{(i)}
x(i),y(i)分别表示样本点
(
x
(
i
)
,
y
(
i
)
)
(x^{(i)},y^{(i)})
(x(i),y(i))的横坐标、纵坐标。此时给定一个样本点
(
x
(
k
)
,
y
(
k
)
)
(x^{(k)},y^{(k)})
(x(k),y(k))(红色样本点)如图所示：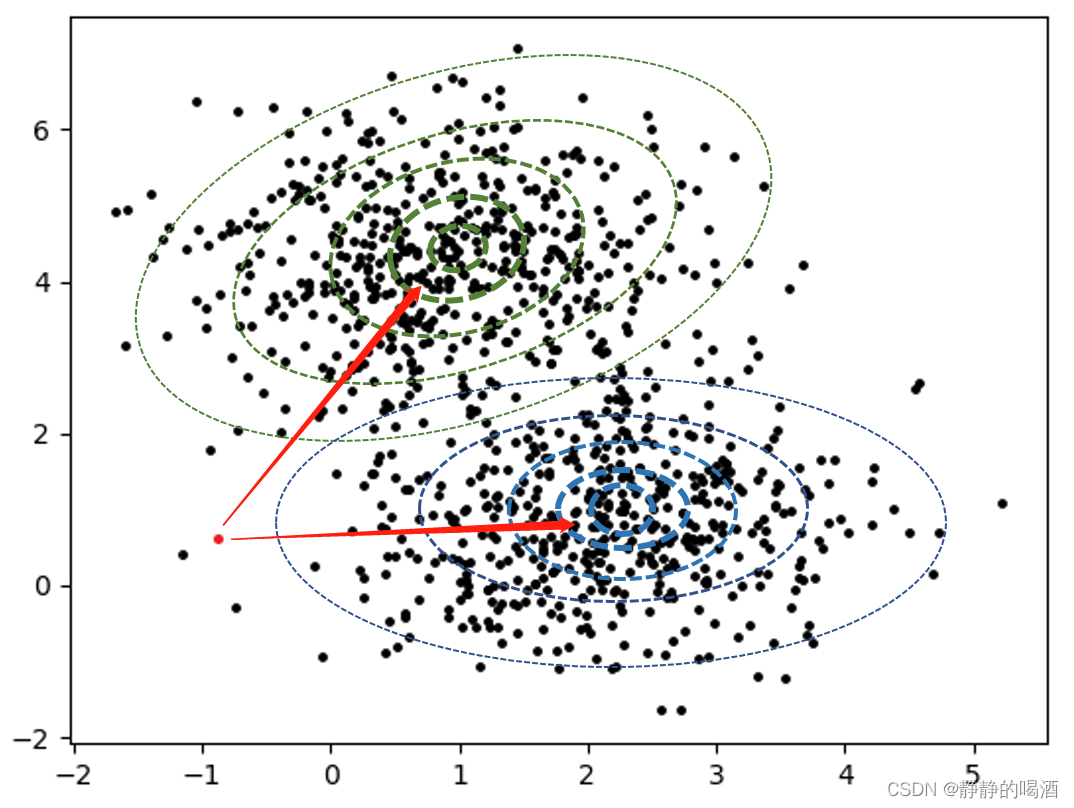 
我们提出的问题是：红色样本点
(
x
(
k
)
,
y
(
k
)
)
(x^{(k)},y^{(k)})
(x(k),y(k))属于哪个高斯分布？ 上述的高斯分布的等高线只是画了若干条以作表示，但实际上高斯分布在其样本空间内无限延伸。 因此，实际上
(
x
(
k
)
,
y
(
k
)
)
(x^{(k)},y^{(k)})
(x(k),y(k))只要在该样本空间内，它属于任意一个高斯分布，但如果需要确定该样本所服从的规律，我们可以提出一个朴素想法： 该样本距离哪个高斯分布中心更近一点，它是哪个高斯分布的概率就更大一点。 基于上述想法，构建一个变量
Z
\mathcal Z
Z，并赋予它实际意义：样本
(
x
(
k
)
,
y
(
k
)
)
(x^{(k)},y^{(k)})
(x(k),y(k))属于哪个高斯分布。 基于上述思想，我们基于变量
Z
\mathcal Z
Z对样本点
(
x
(
k
)
,
y
(
k
)
)
(x^{(k)},y^{(k)})
(x(k),y(k))的分布归属问题有如下判断：
其中， z 1 , z 2 z_1,z_2 z1,z2表示高斯分布编号(离散型随机变量)， p 1 , p 2 p_1,p_2 p1,p2表示样本点 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i))分别属于高斯分布 z 1 , z 2 z_1,z_2 z1,z2的概率。即： p j = P [ ( x ( i ) , y ( i ) ) ∈ z j ] ( j = 1 , 2 ) p_j = P[(x^{(i)},y^{(i)}) \in z_j] \quad (j=1,2) pj=P[(x(i),y(i))∈zj](j=1,2) 关于 P ( Z ) P(\mathcal Z) P(Z)的约束条件有： p 1 + p 2 = 1 p_1 + p_2 = 1 p1+p2=1
概率混合模型的引出基于上述例子，我们称上述定义的变量 Z \mathcal Z Z为隐变量。原因在于该变量无法从样本集合自身观察出来，而定义它的目的在于协助求解概率分布 P ( X ) P(\mathcal X) P(X)。
基于隐变量 Z \mathcal Z Z，可以通过两步走的形式进行求解：
- 对样本点属于样本空间内任意高斯分布的概率进行统计，即求解 P ( Z ) P(\mathcal Z) P(Z);
- 基于步骤1，样本基于各概率服从对应的高斯分布，即求解 P ( X ∣ Z ) P(\mathcal X \mid \mathcal Z) P(X∣Z);
假设样本空间中一共包含
K
\mathcal K
K个高斯分布，概率分布
P
(
X
)
P(\mathcal X)
P(X)可以表示如下： 该式子和‘几何角度’中的公式基本没有区别，只是从不同角度理解理解‘隐变量的表示’而已。
P
(
X
)
=
∑
Z
P
(
X
∣
Z
)
P
(
Z
)
=
∑
k
=
1
K
p
k
⋅
N
(
μ
k
,
Σ
k
)
(
∑
k
=
1
K
p
k
=
1
)
P(\mathcal X) = \sum_{\mathcal Z}P(\mathcal X \mid \mathcal Z)P(\mathcal Z) = \sum_{k=1}^{\mathcal K} p_{k} \cdot \mathcal N(\mu_{k},\Sigma_{k}) \quad (\sum_{k=1}^{\mathcal K} p_k = 1)
P(X)=Z∑P(X∣Z)P(Z)=k=1∑Kpk⋅N(μk,Σk)(k=1∑Kpk=1)
我们在极大似然估计与最大后验概率估计中介绍过， P ( X ) P(\mathcal X) P(X)既可以表示样本集合 X \mathcal X X的概率分布，也可以表示概率模型。
它的描述具体为：样本集合 X \mathcal X X是由概率模型 P ( X ) P(\mathcal X) P(X)生成的样本组成的集合。概率模型可以源源不断地生成样本，样本集合 X \mathcal X X只是其中一个子集。
高斯混合模型的隐变量 Z \mathcal Z Z是一个基于参数的离散分布，因此将高斯混合模型从生成模型的角度 理解为如下步骤：
- 以 p k p_k pk的概率从 K \mathcal K K个离散的参数中选择了参数 k k k；
- 在参数 k k k确定的条件下，由于参数 k k k唯一对应一个高斯分布 N ( μ k , Σ k ) \mathcal N(\mu_k,\Sigma_k) N(μk,Σk)，因此，从高斯分布 N ( μ k , Σ k ) \mathcal N(\mu_k,\Sigma_k) N(μk,Σk)中随机生成一个样本 x x x；
- 重复执行上述步骤，重复 N N N次，最终获得 N N N个样本的样本集合 X \mathcal X X。
下一节将介绍高斯混合模型的求解过程。
相关参考： 机器学习-高斯混合模型（1）-模型介绍
