- 引言
- 回顾:动态概率图模型
- 隐马尔可夫模型
- 场景介绍
- 隐马尔可夫模型的特殊性质
- 齐次马尔可夫假设
- 观测独立性假设
- 隐马尔可夫模型需要解决的任务
上一节对整个概率模型的划分进行了阶段性介绍,本节将系统介绍隐马尔可夫模型(Hidden Markov Model,HMM)。
回顾:动态概率图模型动态概率图模型中的隐变量随着时间/序列信息的变化而变化,如下图所示(右)。相比于静态概率图模型(左),如高斯混合模型,样本点一旦固定下来,对应的隐变量参数不再发生变化。 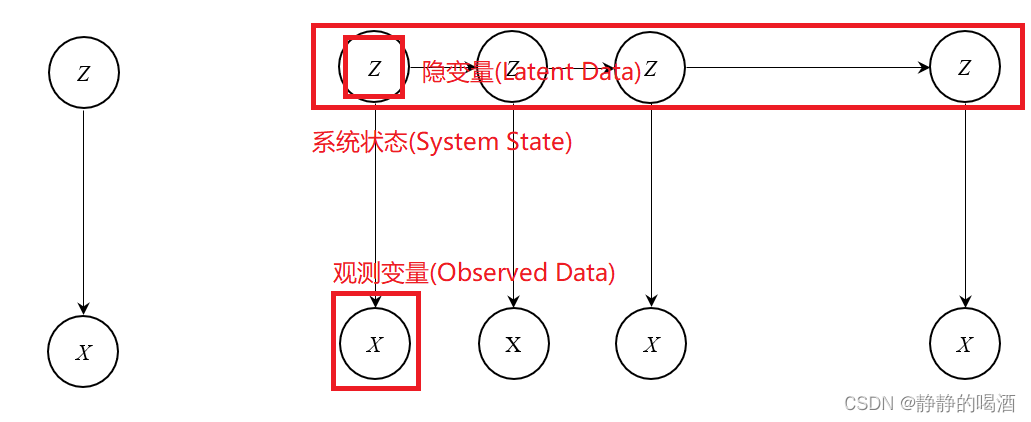
如果 系统状态中的每一个隐变量状态 Z \mathcal Z Z的取值范围是离散的,以系统状态中 t t t时刻对应的隐变量 Z ( t ) \mathcal Z ^{(t)} Z(t)为例, z ( i ) t z^{(i)t} z(i)t表示 t t t时刻的样本点 x ( i ) x^{(i)} x(i)对应的隐变量,存在 K \mathcal K K个离散结果供 z ( i ) t z^{(i)t} z(i)t选择。即: z ( i ) t ∈ { z 1 ( i ) t , z 2 ( i ) t , ⋯ , z K ( i ) t } z^{(i)t} \in \{z_1^{(i)t},z_2^{(i)t},\cdots,z_{\mathcal K}^{(i)t}\} z(i)t∈{z1(i)t,z2(i)t,⋯,zK(i)t} 满足上述条件的动态模型,其代表模型是隐马尔可夫模型。
隐马尔可夫模型 场景介绍对隐马尔可夫模型中出现的概念进行符号定义: 定义 观测变量(Observed Variable)使用符号
O
\mathcal O
O进行表示。各时刻的观测变量表示如下:
O
=
{
o
1
,
o
2
,
⋯
,
o
t
,
o
t
+
1
,
⋯
}
\mathcal O = \{o_1,o_2,\cdots,o_t,o_{t+1},\cdots\}
O={o1,o2,⋯,ot,ot+1,⋯} 同理,定义 状态变量(State Variable)使用符号
I
\mathcal I
I进行表示,各时刻的状态变量表示如下: 指的是隐变量,基于系统状态的另一种表达方式。
I
=
{
i
1
,
i
2
,
⋯
,
i
t
,
i
t
+
1
,
⋯
}
\mathcal I = \{i_1,i_2,\cdots,i_t,i_{t+1},\cdots\}
I={i1,i2,⋯,it,it+1,⋯} 根据上面提到的动态模型,任意时刻的状态变量
i
s
∈
I
(
s
=
1
,
2
,
⋯
,
t
,
t
+
1
,
⋯
)
i_s \in \mathcal I(s = 1,2,\cdots,t,t+1,\cdots)
is∈I(s=1,2,⋯,t,t+1,⋯),其取值范围是离散的,因而定义 状态变量取值范围的离散集合 为
Q
\mathcal Q
Q,并且
Q
\mathcal Q
Q集合中包含
K
\mathcal K
K个元素。具体表示如下:
Q
=
{
q
1
,
q
2
,
⋯
,
q
K
}
\mathcal Q = \{q_1,q_2,\cdots,q_{\mathcal K}\}
Q={q1,q2,⋯,qK} 同理,定义观测变量的取值结果也是离散的,并定义 观测变量取值范围的离散集合 为
V
\mathcal V
V,并且
V
\mathcal V
V集合中包含
M
\mathcal M
M个元素。具体表示如下:
V
=
{
v
1
,
v
2
,
⋯
,
v
M
}
\mathcal V = \{v_1,v_2,\cdots,v_{\mathcal M}\}
V={v1,v2,⋯,vM}
隐马尔可夫模型不同于其他静态模型的表达形式,其概率模型参数 λ \lambda λ表示如下: λ = ( π , A , B ) \lambda = (\pi,\mathcal A,\mathcal B) λ=(π,A,B) 其中:
- π \pi π表示初始状态下的概率分布(Probability Distribution);
- A \mathcal A A表示状态转移矩阵(Transition Matrix);
- B \mathcal B B表示发射矩阵(Emission Matrix)
基于上述定义:
-
状态转移矩阵 A \mathcal A A 表示如下: A = [ a i j ] a i j = P ( i t + 1 = q j ∣ i t = q i ) i , j ∈ { 1 , 2 , ⋯ , K } \mathcal A = [a_{ij}] \quad a_{ij} = P(i_{t+1}=q_j \mid i_t = q_i) \quad i,j \in \{1,2,\cdots,\mathcal K\} A=[aij]aij=P(it+1=qj∣it=qi)i,j∈{1,2,⋯,K} 其中, a i j a_{ij} aij表示状态转移矩阵 A \mathcal A A中 第 i i i行第 j j j列 的元素; P ( i t + 1 = q j ∣ i t = q i ) P(i_{t+1}=q_j \mid i_t = q_i) P(it+1=qj∣it=qi)表示 在 t t t时刻下的状态变量 i t i_t it取值 q i q_i qi的条件下,下一时刻的状态变量 i t + 1 i_{t+1} it+1取值 q j q_j qj的概率。
基于该定义,发现:状态转移矩阵 A \mathcal A A是一个方阵,并且是 K \mathcal K K阶方阵: A = ( a 11 , a 12 , ⋯ , a 1 K a 21 , a 22 , ⋯ , a 2 K ⋮ a K 1 , a K 2 , ⋯ , a K K ) K × K \mathcal A = \begin{pmatrix}a_{11},a_{12},\cdots,a_{1\mathcal K} \\ a_{21},a_{22},\cdots,a_{2\mathcal K} \\ \vdots \\a_{\mathcal K1},a_{\mathcal K2},\cdots,a_{\mathcal K \mathcal K}\end{pmatrix}_{\mathcal K \times \mathcal K} A=⎝ ⎛a11,a12,⋯,a1Ka21,a22,⋯,a2K⋮aK1,aK2,⋯,aKK⎠ ⎞K×K 整个状态转移过程,共用同一个状态转移矩阵 A \mathcal A A,类似于查表。而方阵中的每一个元素均表示一个概率结果。 状态转移过程图像表示如下:
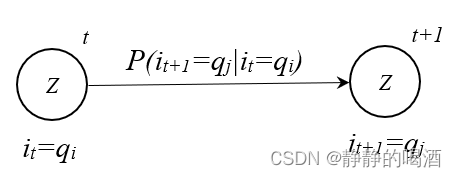
-
同理,发射矩阵 B \mathcal B B 表示如下: B = [ b j ( k ) ] b j ( k ) = P ( o t = v k ∣ i t = q j ) j ∈ { 1 , 2 , ⋯ , K } ; k ∈ { 1 , 2 , ⋯ , M } \mathcal B = [b_{j}(k)] \quad b_j(k) = P(o_t = v_k\mid i_{t} = q_j) \quad j \in \{1,2,\cdots,\mathcal K\};k \in \{1,2,\cdots,\mathcal M\} B=[bj(k)]bj(k)=P(ot=vk∣it=qj)j∈{1,2,⋯,K};k∈{1,2,⋯,M} 其中 b j ( k ) b_j(k) bj(k)表示发射矩阵 B \mathcal B B中的第 j j j行第 k k k列元素; P ( o t = v k ∣ i t = q j ) P(o_t = v_k\mid i_{t} = q_j) P(ot=vk∣it=qj)表示 t t t时刻下状态变量 i t i_t it取值 q j q_j qj的条件下,对应时刻的观测变量 o t o_t ot取值 v k v_k vk的概率。 和状态转移矩阵 A \mathcal A A不同的是,发射矩阵 B \mathcal B B是一个 K × M \mathcal K \times \mathcal M K×M的矩阵: B = ( b 1 ( 1 ) , b 1 ( 2 ) , ⋯ , b 1 ( M ) b 2 ( 1 ) , b 2 ( 2 ) , ⋯ , b 2 ( M ) ⋮ b K ( 1 ) , b K ( 2 ) , ⋯ , b K ( M ) ) K × M \mathcal B = \begin{pmatrix}b_1(1),b_1(2),\cdots,b_1(\mathcal M) \\ b_2(1),b_2(2),\cdots,b_2(\mathcal M) \\ \vdots \\ b_{\mathcal K}(1),b_{\mathcal K}(2),\cdots,b_{\mathcal K}(\mathcal M)\end{pmatrix}_{\mathcal K \times \mathcal M} B=⎝ ⎛b1(1),b1(2),⋯,b1(M)b2(1),b2(2),⋯,b2(M)⋮bK(1),bK(2),⋯,bK(M)⎠ ⎞K×M 同上,每次求解 P ( o t = v k ∣ i t = q j ) P(o_t = v_k\mid i_{t} = q_j) P(ot=vk∣it=qj),均使用同一个发射矩阵。矩阵中的每一个元素也均表示一个概率结果。 状态发射过程图像表示如下:
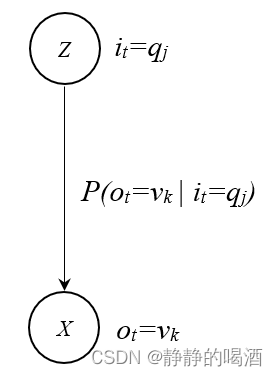
-
π \pi π表示初始时刻的概率分布,当 t = 1 t=1 t=1时,状态 i 1 i_1 i1存在 K \mathcal K K种取值:
需要注意的点:这个初始概率分布是’状态变量‘(隐变量)的初始分布。i 1 ∈ { q 1 , q 2 , ⋯ , q K } i_1 \in \{q_1,q_2,\cdots,q_{\mathcal K}\} i1∈{q1,q2,⋯,qK} 因此, π \pi π表示一个向量,向量元素表示 i 1 i_1 i1取各离散结果 q 1 , q 2 , ⋯ , q K q_1,q_2,\cdots,q_{\mathcal K} q1,q2,⋯,qK的概率值。即: π = ( p 1 p 2 ⋮ p K ) = ( P ( i 1 = q 1 ) P ( i 1 = q 2 ) ⋮ P ( i 1 = q K ) ) K × 1 ∑ k = 1 K P ( i 1 = q k ) = 1 \pi = \begin{pmatrix}p_1 \\p_2 \\ \vdots \\ p_{\mathcal K}\end{pmatrix} = \begin{pmatrix}P(i_1 = q_1) \\ P(i_1 = q_2) \\ \vdots \\P(i_1 = q_{\mathcal K})\end{pmatrix}_{\mathcal K \times 1} \sum_{k=1}^{\mathcal K} P(i_1 = q_k) = 1 π=⎝ ⎛p1p2⋮pK⎠ ⎞=⎝ ⎛P(i1=q1)P(i1=q2)⋮P(i1=qK)⎠ ⎞K×1k=1∑KP(i1=qk)=1
齐次马尔可夫假设的核心是无后效性。它是关于 状态变量 I \mathcal I I后验概率的一个假设。具体表示为:某时刻状态变量 i t + 1 i_{t+1} it+1的后验概率,只和前一时刻的状态变量 i t i_t it相关,与其他变量无关。 数学符号表示如下: P ( i t + 1 ∣ i t , i t − 1 , ⋯ , i 1 , o t , o t − 1 , ⋯ , o 1 ) = P ( i t + 1 ∣ i t ) P(i_{t+1} \mid i_t,i_{t-1},\cdots,i_1,o_t,o_{t-1},\cdots,o_1) = P(i_{t+1} \mid i_t) P(it+1∣it,it−1,⋯,i1,ot,ot−1,⋯,o1)=P(it+1∣it)
观测独立性假设和齐次马尔可夫假设类似,它的核心是观测独立性。并且该假设是关于 观测变量 O \mathcal O O的一个假设。具体表示为: 某时刻观测变量 o t o_{t} ot的后验概率,只和对应时刻的状态变量 i t i_t it相关,与其他变量无关。 P ( o t ∣ i t , i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = P ( o t ∣ i t ) P(o_t \mid i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1) = P(o_t \mid i_t) P(ot∣it,it−1,⋯,i1,ot−1,⋯,o1)=P(ot∣it)
隐马尔可夫模型需要解决的任务- 任务1:求值任务(Evaluation) 具体描述如下:当 λ \lambda λ已知的条件下,即 初始概率分布 π \pi π,状态转移矩阵 A \mathcal A A,发射矩阵 B \mathcal B B 均已知的条件下,一个长度为 T T T的观测序列表示如下: O = { o 1 , o 2 , ⋯ , o T } \mathcal O = \{o_1,o_2,\cdots,o_T\} O={o1,o2,⋯,oT} 求解任务:模型参数 λ \lambda λ已知的条件下,通过该模型求解观测序列 O \mathcal O O发生的概率。即: P ( O ∣ λ ) = P ( o 1 , o 2 , ⋯ , o T ∣ π , A , B ) = ? P(\mathcal O \mid \lambda) = P(o_1,o_2,\cdots,o_T \mid \pi,\mathcal A,\mathcal B) = ? P(O∣λ)=P(o1,o2,⋯,oT∣π,A,B)=? 常用方法是前向算法(Forward Algorithm)与后向算法(Backward Algorithm)。
- 任务2:学习任务(Learning) 即模型参数求解问题,如何通过观测序列求解模型参数 λ = ( π , A , B ) \lambda = (\pi,\mathcal A,\mathcal B) λ=(π,A,B)。即: λ ^ = arg max λ P ( O ∣ λ ) \hat \lambda = \mathop{\arg\max}\limits_{\lambda} P(\mathcal O \mid \lambda) λ^=λargmaxP(O∣λ) 具体算法使用EM算法、Baum-Welch算法。
- 任务3:解码任务(Decoding)(重点) 即给定观测变量序列
O
\mathcal O
O的条件下,找出一组合适的状态变量序列
I
\mathcal I
I,使得
P
(
I
∣
O
)
P(\mathcal I \mid \mathcal O)
P(I∣O)达到最大。即:
I
^
=
arg
max
I
P
(
I
∣
O
)
\hat {\mathcal I} = \mathop{\arg\max}\limits_{\mathcal I} P(\mathcal I \mid \mathcal O)
I^=IargmaxP(I∣O) 将解码任务进行延伸,可以得到两个新的子问题:
- 预测任务(Prediction): 数学符号表达如下: P ( i t + 1 ∣ o 1 , o 2 , ⋯ , o t ) P(i_{t+1} \mid o_1,o_2,\cdots,o_t) P(it+1∣o1,o2,⋯,ot) 文字表达即:给定一条观测变量序列或其中一部分,求出该段观测序列的条件下,下一时刻状态变量的后验概率;
- 滤波任务(Filter): 数学符号表达如下: P ( i t ∣ o 1 , o 2 , ⋯ , o t ) P(i_t \mid o_1,o_2,\cdots,o_t) P(it∣o1,o2,⋯,ot) 即:已知长度为 t t t的观测序列或者某观测序列长度为 t t t的一部分,求解 t t t时刻的状态变量 i t i_t it。
下一节将介绍隐马尔可夫模型的求值问题 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)。
相关参考: 机器学习-隐马尔可夫模型1 -背景介绍 机器学习-隐马尔可夫模型2 -背景介绍



