机器学习笔记之概率图模型(三)贝叶斯网络之有向分离(D划分)

引言

上一节介绍了贝叶斯网络以及贝叶斯网络中条件独立性的识别：同父结构、顺序结构、 V \mathcal V V型结构。本节将介绍判别变量/特征之间是否具备条件独立性的方法—— D \mathcal D D划分。

回顾：贝叶斯网络的局部结构

在条件独立性的识别部分，介绍了三种贝叶斯网络中三个变量/特征之间的典型依赖关系：同父结构(Common Parent)、顺序结构、 V \mathcal V V型结构(V-Structure)。

同父结构(Common Parent)

同父结构的变量依赖关系表示如下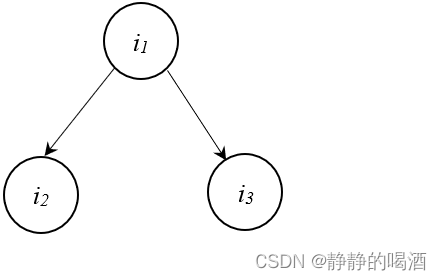： 同父结构中变量/特征 i 1 , i 2 , i 3 i_1,i_2,i_3 i1,i2,i3之间的依赖关系可表示为：给定父结点 i 1 i_1 i1取值的条件下， i 2 , i 3 i_2,i_3 i2,i3之间条件独立。对应数学符号表示如下： i 2 ⊥ i 3 ∣ i 1 P ( i 2 , i 3 ∣ i 1 ) = P ( i 3 ∣ i 1 ) ⋅ P ( i 2 ∣ i 1 ) i_2 \perp i_3 \mid i_1 \\ \mathcal P(i_2,i_3 \mid i_1) = \mathcal P(i_3 \mid i_1) \cdot \mathcal P(i_2 \mid i_1) i2⊥i3∣i1P(i2,i3∣i1)=P(i3∣i1)⋅P(i2∣i1)

顺序结构

顺序结构的变量依赖关系表示如下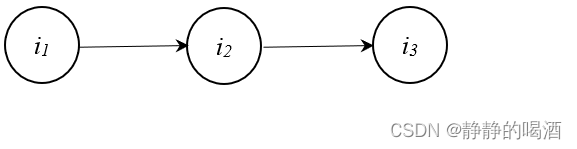： 顺序结构中变量/特征 i 1 , i 2 , i 3 i_1,i_2,i_3 i1,i2,i3之间的依赖关系可表示为：给定结点 i 2 i_2 i2取值的条件下， i 1 , i 3 i_1,i_3 i1,i3之间条件独立。对应数学符号表示如下： i 1 ⊥ i 3 ∣ i 2 P ( i 1 , i 3 ∣ i 2 ) = P ( i 3 ∣ i 2 ) ⋅ P ( i 1 ∣ i 2 ) i_1 \perp i_3 \mid i_2 \\ \mathcal P(i_1,i_3 \mid i_2) = \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_1 \mid i_2) i1⊥i3∣i2P(i1,i3∣i2)=P(i3∣i2)⋅P(i1∣i2)

V \mathcal V V型结构(V-Structure)

V \mathcal V V型结构的变量依赖关系表示如下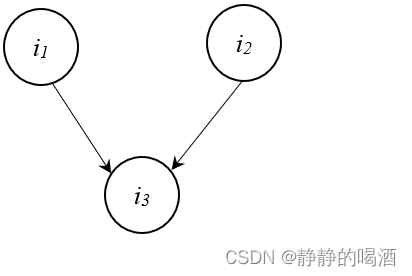： V \mathcal V V型结构中变量/特征 i 1 , i 2 , i 3 i_1,i_2,i_3 i1,i2,i3之间的依赖关系可表示为：若 i 3 i_3 i3取值未知的条件下， i 1 , i 2 i_1,i_2 i1,i2之间条件独立；若给定 i 3 i_3 i3取值的条件下， i 1 , i 2 i_1,i_2 i1,i2必不独立。对应数学符号表示如下： P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_3 \mid i_1,i_2) P(i3∣i1,i2)即表示 i 3 i_3 i3是在 i 1 , i 2 i_1,i_2 i1,i2给定的条件下，以‘条件概率’形式表现出的未知状态。 P ( i 3 ∣ i 1 , i 2 ) → P ( i 2 ) = P ( i 2 ∣ i 1 ) \mathcal P(i_3 \mid i_1,i_2) \to \mathcal P(i_2) = \mathcal P(i_2 \mid i_1) P(i3∣i1,i2)→P(i2)=P(i2∣i1)

关于贝叶斯网络局部结构的补充

关于 V \mathcal V V型结构中的条件独立性，譬如：某变量 C \mathcal C C未知的条件下，变量 A \mathcal A A与变量 B \mathcal B B之间相互独立的情况，满足这种情况的条件独立性也称边际独立性(Marginal Independence)。数学符号表示如下： 这种独立性区别于‘一般的条件独立性’ i 1 ⊥ i 2 i_1 \perp i_2 i1⊥i2。 P ( i 3 ∣ i 1 , i 2 ) → P ( i 2 ) = P ( i 2 ∣ i 1 ) i 1 ⊥  ⁣ ⁣ ⁣ ⁣ ⊥ i 2 \mathcal P(i_3 \mid i_1,i_2) \to \mathcal P(i_2) = \mathcal P(i_2 \mid i_1) \\ i_1 \perp\!\!\!\!\perp i_2 P(i3∣i1,i2)→P(i2)=P(i2∣i1)i1⊥⊥i2

一个变量的取值与否，是否对另外两个变量的独立性产生影响，这个现象并不是 V \mathcal V V型结构特有的现象。

事实上，同父结构、顺序结构同样也存在这种现象：

• 同父结构：
  • 给定结点 i 1 i_1 i1取值的条件下， i 2 , i 3 i_2,i_3 i2,i3之间条件独立。即 i 2 ⊥ i 3 ∣ i 1 i_2 \perp i_3 \mid i_1 i2⊥i3∣i1成立；
  • (相反)结点 i 1 i_1 i1取值未知的条件下， i 2 , i 3 i_2,i_3 i2,i3之间条件不独立。即 i 2 ⊥  ⁣ ⁣ ⁣ ⁣ ⊥ i 3 i_2 \perp\!\!\!\!\perp i_3 i2⊥⊥i3不成立。
• 顺序结构：
  • 给定结点 i 2 i_2 i2取值的条件下， i 1 , i 3 i_1,i_3 i1,i3之间条件独立。即 i 1 ⊥ i 3 ∣ i 2 i_1 \perp i_3 \mid i_2 i1⊥i3∣i2成立；
  • (相反)结点 i 2 i_2 i2取值未知的条件下， i 1 , i 3 i_1,i_3 i1,i3之间条件不独立。即 i 1 ⊥  ⁣ ⁣ ⁣ ⁣ ⊥ i 3 i_1 \perp\!\!\!\!\perp i_3 i1⊥⊥i3不成立。

如果将贝叶斯网络结构再复杂一些。如下图表示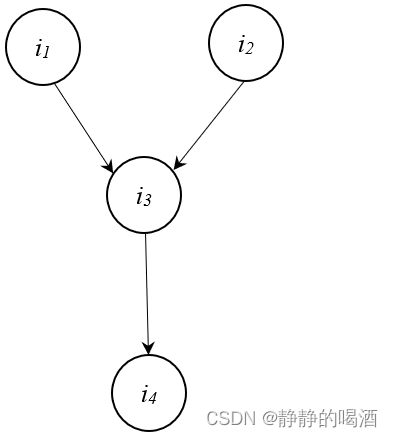： 讨论：变量 i 4 i_4 i4取值的确定与否，对 i 1 , i 2 i_1,i_2 i1,i2两个变量间的独立性发生什么影响？ 推导过程如下：

• 通过因子分解描述该形状的联合概率分布 P ( i 1 , i 2 , i 3 , i 4 ) \mathcal P(i_1,i_2,i_3,i_4) P(i1,i2,i3,i4)： P ( i 1 , i 2 , i 3 , i 4 ) = P ( i 1 ) ⋅ P ( i 2 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 3 ) \mathcal P(i_1,i_2,i_3,i_4) = \mathcal P(i_1) \cdot \mathcal P(i_2) \cdot \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_3) P(i1,i2,i3,i4)=P(i1)⋅P(i2)⋅P(i3∣i1,i2)⋅P(i4∣i3)
• 通过联合概率分布的链式法则求解联合概率分布 P ( i 1 , i 2 , i 3 , i 4 ) \mathcal P(i_1,i_2,i_3,i_4) P(i1,i2,i3,i4)： P ( i 1 , i 2 , i 3 , i 4 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 1 , i 2 , i 3 ) \mathcal P(i_1,i_2,i_3,i_4) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_1,i_2,i_3) P(i1,i2,i3,i4)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2)⋅P(i4∣i1,i2,i3)
• 上述两个公式描述的是同一概率分布，则有： P ( i 1 ) ⋅ P ( i 2 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 1 , i 2 , i 3 ) \mathcal P(i_1) \cdot \mathcal P(i_2) \cdot \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_1,i_2,i_3) P(i1)⋅P(i2)⋅P(i3∣i1,i2)⋅P(i4∣i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2)⋅P(i4∣i1,i2,i3) 经过化简，则有： P ( i 2 ) ⋅ P ( i 4 ∣ i 3 ) = P ( i 2 ∣ i 1 ) ⋅ P ( i 4 ∣ i 1 , i 2 , i 3 ) \mathcal P(i_2) \cdot \mathcal P(i_4 \mid i_3) = \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_4 \mid i_1,i_2,i_3) P(i2)⋅P(i4∣i3)=P(i2∣i1)⋅P(i4∣i1,i2,i3)
• 根据贝叶斯网络，观察：结点 i 4 i_4 i4只和 i 3 i_3 i3存在直接关联关系，而与 i 1 , i 2 i_1,i_2 i1,i2无直接关联关系。因而有： 由于无直接关联关系， i 2 , i 3 i_2,i_3 i2,i3是否给定，对 i 4 i_4 i4的条件概率结果不产生影响。 P ( i 4 ∣ i 3 ) = P ( i 4 ∣ i 1 , i 2 , i 3 ) \mathcal P(i_4 \mid i_3) = \mathcal P(i_4 \mid i_1,i_2,i_3) P(i4∣i3)=P(i4∣i1,i2,i3) 将该式代入上式中，则有： P ( i 2 ) = P ( i 2 ∣ i 1 ) \mathcal P(i_2) = \mathcal P(i_2 \mid i_1) P(i2)=P(i2∣i1)

由于 P ( i 2 ) = P ( i 2 ∣ i 1 ) \mathcal P(i_2) = \mathcal P(i_2 \mid i_1) P(i2)=P(i2∣i1)是基于 P ( i 4 ∣ i 3 ) = P ( i 4 ∣ i 1 , i 2 , i 3 ) \mathcal P(i_4 \mid i_3) = \mathcal P(i_4 \mid i_1,i_2,i_3) P(i4∣i3)=P(i4∣i1,i2,i3)条件下成立的，基于上一节 V \mathcal V V型结构的规律， i 4 i_4 i4在‘|’前面，说明 i 4 i_4 i4是未知状态。

因而有如下表达：在结点 i 4 i_4 i4取值未知的情况下， i 1 , i 2 i_1,i_2 i1,i2相互独立；相反，结点 i 4 i_4 i4给定的条件下， i 1 , i 2 i_1,i_2 i1,i2必不独立。 i 4 i_4 i4结点与 i 3 i_3 i3结点存在‘相同的性质’~

D \mathcal D D划分(D-Separation)

D \mathcal D D划分是 判断有向图中变量(变量集合)间是否存在条件独立性 的一种方法。

D \mathcal D D划分本质上是上述示例的更普遍、更泛化的方法表示。某样本集合 X \mathcal X X的特征 ( x 1 , x 2 , ⋯ , x p ) (x_1,x_2,\cdots,x_p) (x1,x2,⋯,xp)划分为如下三个变量集合： x A , x B , x C x_{\mathcal A},x_{\mathcal B},x_{\mathcal C} xA,xB,xC 并且 x A , x B , x C x_{\mathcal A},x_{\mathcal B},x_{\mathcal C} xA,xB,xC集合内元素互不相交。 如何基于上述三个集合描述条件独立性： x A ⊥ x C ∣ x B x_{\mathcal A} \perp x_{\mathcal C} \mid x_{\mathcal B} xA⊥xC∣xB

使用文字方式描述上述条件独立性：当变量集合 x B x_{\mathcal B} xB中的特征给定的条件下，变量集合 x A x_{\mathcal A} xA和变量集合 x C x_{\mathcal C} xC中的特征相互独立。

场景构建：

• 假设 l a l_a la是变量集合 x A x_{\mathcal A} xA中的一个变量/特征；
• l c l_c lc是变量集合 x C x_{\mathcal C} xC中的一个变量/特征；
• 并且在贝叶斯网络中 l a , l c l_a,l_c la,lc之间存在边，并且边上存在一个非 l a , l c l_a,l_c la,lc的变量/特征构成的结点，定义其为 l b l_{b} lb： 个人理解：D划分只是一个泛化的表示，我们只能判定‘若结点之间相互独立 -> '该对结点'必不在同一集合中(即相互独立)；但是并不能判定'某对结点'在一个集合中。’

D \mathcal D D划分对三种局部结构的描述表示如下：

• 如果 l a , l b , l c l_a,l_b,l_c la,lb,lc满足同父结构，有： l b l_b lb必存在于 x B x_{\mathcal B} xB集合中。图像表示如下： 只有 l b ∈ x B l_b \in x_{\mathcal B} lb∈xB时，在给定集合 x B x_{\mathcal B} xB中的各特征时， l b l_b lb才会被给定，从而实现 l a , l c l_a,l_c la,lc相互独立： l a ⊥ l c ∣ l b l_a \perp l_c \mid l_b la⊥lc∣lb 如果对于 ∀ l a ∈ x A , ∀ l c ∈ x C \forall l_a \in x_{\mathcal A},\forall l_c \in x_{\mathcal C} ∀la∈xA,∀lc∈xC满足：

  • l a , l c l_a,l_c la,lc之间存在边，并且边上存在一个非 l a , l c l_a,l_c la,lc的变量/特征构成的结点 l b l_b lb，且构成同父结构；
  • l b ∈ x B l_b \in x_{\mathcal B} lb∈xB；

  则有： x A ⊥ x C ∣ x B x_{\mathcal A} \perp x_{\mathcal C} \mid x_{\mathcal B} xA⊥xC∣xB

• 如果 l a , l b , l c l_a,l_b,l_c la,lb,lc满足顺序结构，有： l b l_b lb必存在于 x B x_{\mathcal B} xB集合中。图像表示如下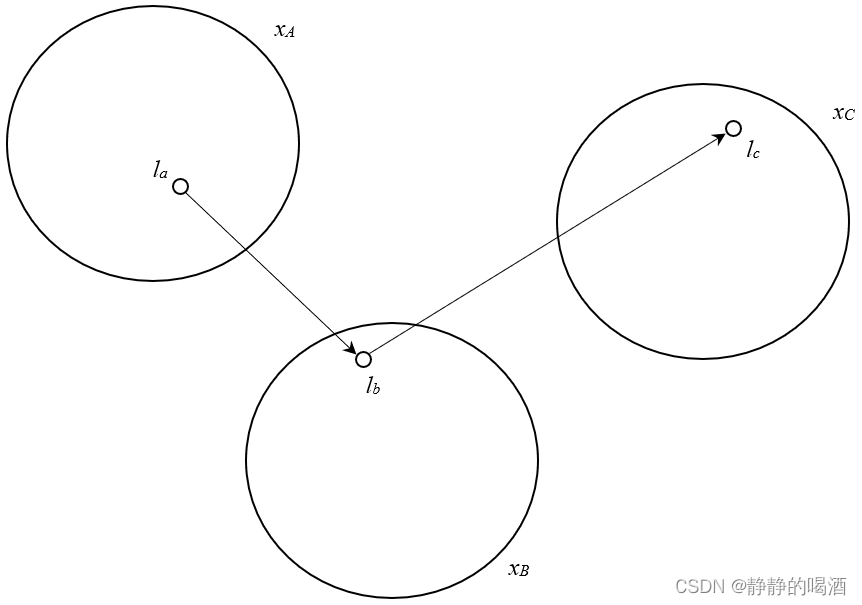： 如果 ∀ l a ∈ x A , ∀ l c ∈ x C \forall l_a \in x_{\mathcal A},\forall l_c \in x_{\mathcal C} ∀la∈xA,∀lc∈xC满足：

  • l a , l c l_a,l_c la,lc之间存在边，并且边上存在一个非 l a , l c l_a,l_c la,lc的变量/特征构成的结点 l b l_b lb，且构成顺序结构；
  • l b ∈ x B l_b \in x_{\mathcal B} lb∈xB；

  则有： x A ⊥ x C ∣ x B x_{\mathcal A} \perp x_{\mathcal C} \mid x_{\mathcal B} xA⊥xC∣xB

• 如果 l a , l b , l c l_a,l_b,l_c la,lb,lc满足 V \mathcal V V型结构，不同于上述两种结构，此时： l b l_b lb必不存在于 x B x_{\mathcal B} xB集合中。图像表示如下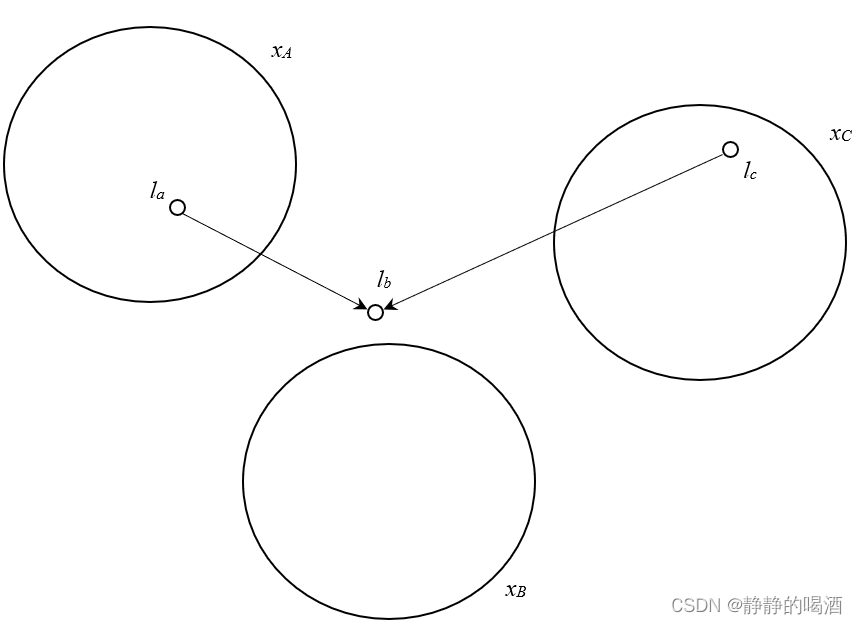： 如果此时再次给定 x B x_{\mathcal B} xB集合中的特征时，由于 l b ∉ x B l_b \notin x_{\mathcal B} lb∈/xB，从而 l b l_b lb没有被给定，根据 V \mathcal V V型结构的定义，使得 l a , l c l_a,l_c la,lc相互独立。 如果 ∀ l a ∈ x A , ∀ l c ∈ x C \forall l_a \in x_{\mathcal A},\forall l_c \in x_{\mathcal C} ∀la∈xA,∀lc∈xC满足：

  • l a , l c l_a,l_c la,lc之间存在边，并且边上存在一个非 l a , l c l_a,l_c la,lc的变量/特征构成的结点 l b l_b lb，且构成 V \mathcal V V型结构；
  • l b ∉ x B l_b \notin x_{\mathcal B} lb∈/xB；

  则有： x A ⊥ x C ∣ x B x_{\mathcal A} \perp x_{\mathcal C} \mid x_{\mathcal B} xA⊥xC∣xB

• 如果 l a , l b , l c l_a,l_b,l_c la,lb,lc满足 V \mathcal V V型结构， l b l_b lb结点存在一个或多个子节点，有： l b l_b lb及其子结点均不存在于 x B x_{\mathcal B} xB集合中。图像表示如下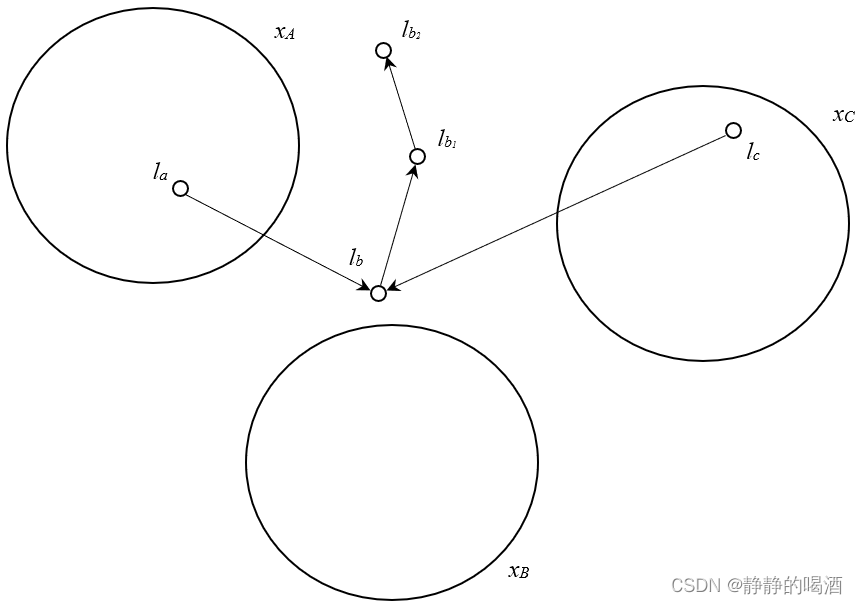： 在上面的推导中证明了 l b l_b lb的子节点和 l b l_b lb存在相同性质。如果 ∀ l a ∈ x A , ∀ l c ∈ x C \forall l_a \in x_{\mathcal A},\forall l_c \in x_{\mathcal C} ∀la∈xA,∀lc∈xC满足：

  • l a , l c l_a,l_c la,lc之间存在边，并且边上存在一个非 l a , l c l_a,l_c la,lc的变量/特征构成的结点 l b l_b lb，构成 V \mathcal V V型结构，并且 l b l_b lb存在子节点 l b 1 , l b 2 , ⋯ l_{b_1},l_{b_2},\cdots lb1,lb2,⋯；
  • l b , l b 1 , l b 2 , ⋯ ∉ x B l_b,l_{b_1},l_{b_2},\cdots \notin x_{\mathcal B} lb,lb1,lb2,⋯∈/xB；

  则有： x A ⊥ x C ∣ x B x_{\mathcal A} \perp x_{\mathcal C} \mid x_{\mathcal B} xA⊥xC∣xB

当然，在真实环境中，大概率不存在只包含一种结构，更多的是上述几种结构的混合形式。每种结构均包含2个条件，按照对应条件进行判定即可。

这种判定规则被称为全局马尔可夫性(Global Markov Property)：给定两个变量子集的分离集(Separating Set)，则两个变量子集相互独立。 这里是‘贝叶斯网络’对‘全局马尔可夫性’的使用，后续在马尔可夫随机场中会继续介绍。

D \mathcal D D划分与道德图

为了分析贝叶斯网络中各变量间的条件独立性，我们需要使用 D \mathcal D D划分将有向图转化为无向图：

• 找出贝叶斯网络中所有的 V \mathcal V V型结构，并将 V \mathcal V V型结构的两个父结点加上一条无向边；
• 将图中所有的有向边改为无向边；

示例：以西瓜书P157页的有向图进行修改。具体图像表示如下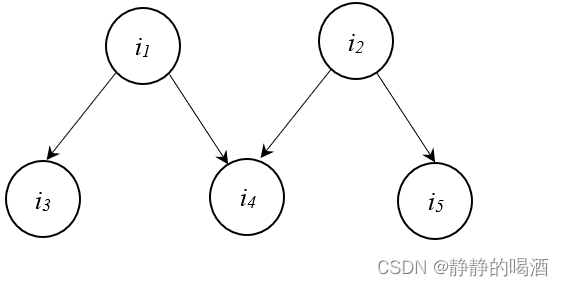： 观察：上图中一共包含一个 V \mathcal V V型结构，两个同父结构。将 V \mathcal V V型结构的两个父节点 i 1 , i 2 i_1,i_2 i1,i2用无向边相连，再将有向边改为无向边，最终结果表示如下：

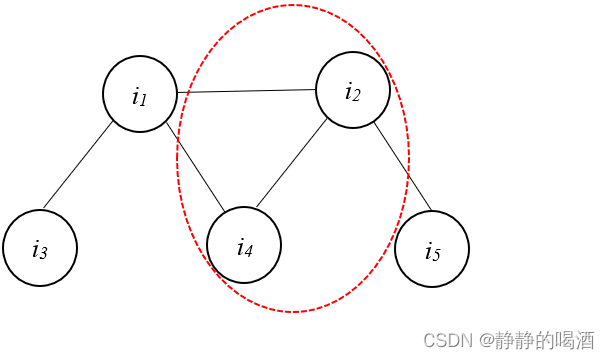
上述转化后的图结果被称作道德图(Moral Graph)。名字含义即：子节点的父母(子节点的两个父节点)要建立牢固的关联关系。

道德图能够直观地找到变量间的条件独立性。假设图中红圈部分称为变量集合 Z \mathcal Z Z，在变量集合 Z \mathcal Z Z被观测的情况下，变量 i 1 , i 5 i_1,i_5 i1,i5能够被变量集合 Z \mathcal Z Z分开，即将变量集合 Z \mathcal Z Z去除后， i 1 , i 5 i_1,i_5 i1,i5分属两个不同的连通分支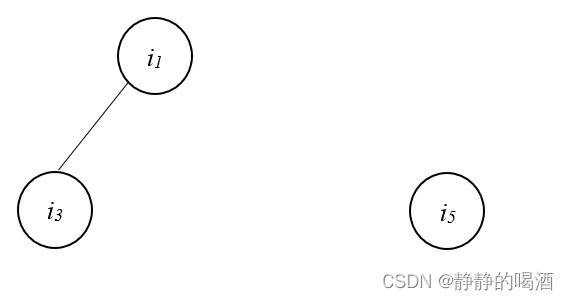： 称 i 1 , i 5 i_1,i_5 i1,i5被变量集合 Z \mathcal Z Z有向分离( D \mathcal D D划分)。由于无向图不存在类似于有向图的各种结构，因此可以直观地找到所有条件独立关系。如 i 1 ⊥ i 5 ∣ i 2 , i 3 ⊥ i 5 ∣ i 2 i_1 \perp i_5 \mid i_2,i_3 \perp i_5 \mid i_2 i1⊥i5∣i2,i3⊥i5∣i2等。 i 3 ⊥ i 5 ∣ i 2 i_3 \perp i_5 \mid i_2 i3⊥i5∣i2关系更加特殊一些。因为它们之间的路径上存在多个变量： i 3 → i 1 → i 2 → i 5 i 3 → i 1 → i 4 → i 2 → i 5 i_3 \to i_1 \to i_2 \to i_5 \\ i_3 \to i_1 \to i_4\to i_2 \to i_5 i3→i1→i2→i5i3→i1→i4→i2→i5

但每个路径都存在被观测的节点。因此在道德图中，整个路径中只要存在节点被观测，对应结点之间必然相互独立。

从关联关系的角度认识道德图

道德图产生的想法是：将有向图转为无向图。产生这种想法的原因在于：相比于有向图，无向图对于关联关系的表达虽然没有有向图精确，但更加泛化。

有向图表示的是显式的因果关系，谁是给定条件，谁是未知，一目了然： P ( X ) = ∏ i = 1 p P ( x i ∣ x p a ( i ) ) \mathcal P(\mathcal X) = \prod_{i=1}^p \mathcal P(x_i \mid x_{pa(i)}) P(X)=i=1∏pP(xi∣xpa(i)) 无向图表示的是存在的相关性，相比于有向图，它表示的结果更加宽泛，没有具体的指向关系： x C i x_{\mathcal C_i} xCi表示最大团。团的相关描述见‘马尔可夫随机场’传送门 P ( X ) = 1 Z ∏ i = 1 K ψ ( x C i ) \mathcal P(\mathcal X) = \frac{1}{\mathcal Z} \prod_{i=1}^{\mathcal K} \psi(\mathcal x_{\mathcal C_i}) P(X)=Z1i=1∏Kψ(xCi) 在后续推断过程中，不需要界定其是有向图还是无向图。在信念传播介绍中马尔可夫链结构的红蓝箭头就是这种表示。

此时，回顾贝叶斯网络中的三种结构：同父结构、顺序结构、 V \mathcal V V型结构。如果将三种结构的箭头去掉，只存在一种结构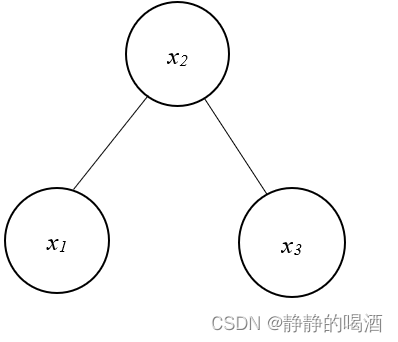： 并不是说有向图转化为无向图，仅将箭头去掉就可以了，需要观察箭头去掉之后，对应的无向图是否影响原来结构结点之间的条件独立性。

同父结构与对应道德图

观察同父结构与对应道德图对于联合概率分布 P ( x 1 , x 2 , x 3 ) \mathcal P(x_1,x_2,x_3) P(x1,x2,x3)的表示对比： { P ( x 1 , x 2 , x 3 ) = P ( x 2 ) ⋅ P ( x 1 ∣ x 2 ) ⋅ P ( x 3 ∣ x 2 ) P ( x 1 , x 2 , x 3 ) = 1 Z ψ 12 ( x 1 , x 2 ) ⋅ ψ 23 ( x 2 , x 3 ) \begin{cases} \mathcal P(x_1,x_2,x_3) = \mathcal P(x_2) \cdot \mathcal P(x_1 \mid x_2) \cdot \mathcal P(x_3 \mid x_2) \\ \mathcal P(x_1,x_2,x_3) = \frac{1}{\mathcal Z} \psi_{12}(x_1,x_2) \cdot \psi_{23}(x_2,x_3) \end{cases} {P(x1,x2,x3)=P(x2)⋅P(x1∣x2)⋅P(x3∣x2)P(x1,x2,x3)=Z1ψ12(x1,x2)⋅ψ23(x2,x3) 从结点变量的角度，可以对有向图结果进行划分： 并准确地描述了 x 1 , x 3 x_1,x_3 x1,x3之间的条件独立性。因为在道德图中， x 1 , x 3 x_1,x_3 x1,x3分别属于不同的最大团。 { P ( x 2 ) ⋅ P ( x 1 ∣ x 2 ) → ψ 12 ( x 1 , x 2 ) P ( x 3 ∣ x 2 ) → ψ 23 ( x 2 , x 3 ) \begin{cases} \mathcal P(x_2) \cdot \mathcal P(x_1 \mid x_2) \to \psi_{12}(x_1,x_2)\\ \mathcal P(x_3\mid x_2) \to \psi_{23}(x_2,x_3) \end{cases} {P(x2)⋅P(x1∣x2)→ψ12(x1,x2)P(x3∣x2)→ψ23(x2,x3)

顺序结构与对应道德图

观察顺序结构与对应盗的图对于联合概率分布 P ( x 1 , x 2 , x 3 ) \mathcal P(x_1,x_2,x_3) P(x1,x2,x3)的表示对比： { P ( x 1 , x 2 , x 3 ) = P ( x 1 ) ⋅ P ( x 2 ∣ x 1 ) ⋅ P ( x 3 ∣ x 2 ) P ( x 1 , x 2 , x 3 ) = 1 Z ψ 12 ( x 1 , x 2 ) ⋅ ψ 23 ( x 2 , x 3 ) \begin{cases} \mathcal P(x_1,x_2,x_3) = \mathcal P(x_1) \cdot \mathcal P(x_2 \mid x_1) \cdot \mathcal P(x_3 \mid x_2) \\ \mathcal P(x_1,x_2,x_3) = \frac{1}{\mathcal Z} \psi_{12}(x_1,x_2) \cdot \psi_{23}(x_2,x_3) \end{cases} {P(x1,x2,x3)=P(x1)⋅P(x2∣x1)⋅P(x3∣x2)P(x1,x2,x3)=Z1ψ12(x1,x2)⋅ψ23(x2,x3) 在划分的过程中，从结点变量的角度，可以对有向图结果进行划分： ‘顺序结构’与‘同父结构’的条件独立性相同，因此，也可以将变量分别正确的划分进两个最大团中。 { P ( x 1 ) ⋅ P ( x 2 ∣ x 1 ) → ψ 12 ( x 1 , x 2 ) P ( x 3 ∣ x 2 ) → ψ 23 ( x 2 , x 3 ) \begin{cases} \mathcal P(x_1) \cdot \mathcal P(x_2 \mid x_1) \to \psi_{12}(x_1,x_2) \\ \mathcal P(x_3\mid x_2) \to \psi_{23}(x_2,x_3) \end{cases} {P(x1)⋅P(x2∣x1)→ψ12(x1,x2)P(x3∣x2)→ψ23(x2,x3)

V \mathcal V V型结构与对应道德图

观察 V \mathcal V V型结构与对应道德图对于联合概率分布 P ( x 1 , x 2 , x 3 ) \mathcal P(x_1,x_2,x_3) P(x1,x2,x3)的表示对比： { P ( x 1 , x 2 , x 3 ) = P ( x 1 ) ⋅ P ( x 3 ) ⋅ P ( x 1 , x 3 ∣ x 2 ) P ( x 1 , x 2 , x 3 ) = 1 Z ψ 12 ( x 1 , x 2 ) ⋅ ψ 23 ( x 2 , x 3 ) \begin{cases} \mathcal P(x_1,x_2,x_3) = \mathcal P(x_1) \cdot \mathcal P(x_3) \cdot \mathcal P(x_1,x_3 \mid x_2)\\ \mathcal P(x_1,x_2,x_3) = \frac{1}{\mathcal Z} \psi_{12}(x_1,x_2) \cdot \psi_{23}(x_2,x_3) \end{cases} {P(x1,x2,x3)=P(x1)⋅P(x3)⋅P(x1,x3∣x2)P(x1,x2,x3)=Z1ψ12(x1,x2)⋅ψ23(x2,x3)

注意： P ( x 1 , x 3 ∣ x 2 ) \mathcal P(x_1,x_3 \mid x_2) P(x1,x3∣x2)一项中就包含了三个变量，这意味着它对应的无向图结果中必须包含三个变量结点的团结构。 这也暗含‘V型结构’的描述：给定 x 2 x_2 x2条件下， x 1 , x 3 x_1,x_3 x1,x3必不独立。

但实际上对应无向图中最多只包含两个结点的团，这说明：仅仅通过去掉有向图的箭头，无法表示 V \mathcal V V型结构的条件独立性关系。

如何对有向图进行改进，使其能够表示 V \mathcal V V型结构的条件独立性，即在两个父结点之间连接一条边，使三个变量结点组成一个极大团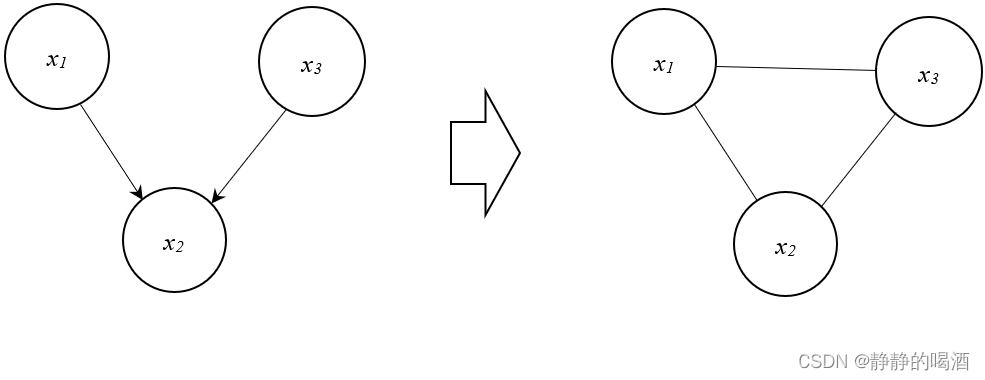： 观察改进后的道德图与 V \mathcal V V型结构： 最大团发生了变化。 P ( x 1 , x 2 , x 3 ) = 1 Z ψ 123 ( x 1 , x 2 , x 3 ) ψ 123 ( x 1 , x 2 , x 3 ) → P ( x 1 ) ⋅ P ( x 3 ) ⋅ P ( x 1 , x 3 ∣ x 2 ) \mathcal P(x_1,x_2,x_3) = \frac{1}{\mathcal Z} \psi_{123}(x_1,x_2,x_3) \\ \psi_{123}(x_1,x_2,x_3) \to \mathcal P(x_1) \cdot \mathcal P(x_3) \cdot \mathcal P(x_1,x_3 \mid x_2) P(x1,x2,x3)=Z1ψ123(x1,x2,x3)ψ123(x1,x2,x3)→P(x1)⋅P(x3)⋅P(x1,x3∣x2)

因此，将有向图转化为无向图时，仅对 V \mathcal V V型结构进行修改。

相关参考： 机器学习 - 周志华著 机器学习-概率图模型3-贝叶斯网络-Representation-D-Separation 机器学习-概率图模型-概念补充-道德图（Moral Graph）