可持久化线段树 主席树 详解

😊 | Powered By HeartFireY | Persistent Segment Tree 📕 | 需要的前导知识：线段树(Segment Tree)、权值线段树、可持久化数据结构理论(Persistent Data Structure Theory) 一、可持久化线段树 简介

可持久化线段树，顾名思义，即对线段树进行可持久化处理之后的线段树。

在可持久化数据结构的理论中，我们对可持久化的概念有所了解：“可以返回之前的某个状态，并在该基础上进行修改”。可持久化线段树就是这样一种结构。

我们从一般思路出发进行分析：想要让线段树可持久化，最朴素的方法就是每进行一次操作都新建一颗线段树。但显然这是不明智的做法：时间和空间上而言都是非常差的的算法。我们不妨继续分析一下更新之后与更新之前的结构：每次更新都只有少量的点被修改。因此大量的点可以继续使用，无需重新建树。

本文分两个部分对可持久化线段树进行探讨。

值得注意的是：我们一般认为主席树就是可持久化线段树，实际上两者之间有区分：

可持久化线段树单纯指经过可持久化处理之后，能够查询、修改历史节点数据的结构，建立在基础线段树的基础之上；而主席树建立在权值线段树的基础之上，能够查询修改历史节点。二者本质区别在于纪念性可持久化的对象所维护的对象不同(一个维护权值、一个维护值域)。

因此，可持久化线段树 ≠ \neq ​=主席树，准确的说，主席树 ⊂ \subset ⊂可持久化线段树。

二、可持久化线段树 基本结构与操作 1.基本结构、建树操作

首先应该明确一点：由于可持久化结构重叠的特殊性，可持久化线段树不能采用堆式储存，因此只能采取动态开点的方式进行储存。

不同于后续节点的更新，对于最初的状态下的线段树我们采用一次建树完成：

1. 采用递归建树，递归函数参数保存左右边界(初始化为 ( 1 , n ) (1, n) (1,n))、当前元素的指针。同时保存总计数 c n t cnt cnt；

2. 递归边界控制为 l = = r l == r l==r，由于此时左边界 l l l即为指向 a a a数组的指针，因此叶子节点赋值 v a l ( p ) = a [ l ] val(p) = a[l] val(p)=a[l] ；

3. 非叶子节点首先记录左右子节点的下标 l s ( p ) = c n t + + , r s ( p ) = c n t + + ls(p) = cnt++, rs(p) = cnt++ ls(p)=cnt++,rs(p)=cnt++，然后递归建左右子树：

   b u i l d ( l ,   m i d ,   l s ( p ) ) 、 b u i l d ( m i d + 1 ,   r ,   r s ( p ) ) build(l,\ mid,\ ls(p))、build(mid + 1, \ r,\ rs(p)) build(l, mid, ls(p))、build(mid+1, r, rs(p))

4. 建立左右节点后非叶子节点 = 左右子节点的和： v a l ( p ) = v a l ( l s ( p ) ) + v a l ( r s ( p ) ) val(p) = val(ls(p)) + val(rs(p)) val(p)=val(ls(p))+val(rs(p))

根据以上建树过程，我们以数组 a = 1 , 2 , 3 , 4 , 5 a = {1,2,3,4,5} a=1,2,3,4,5为例建立线段树：

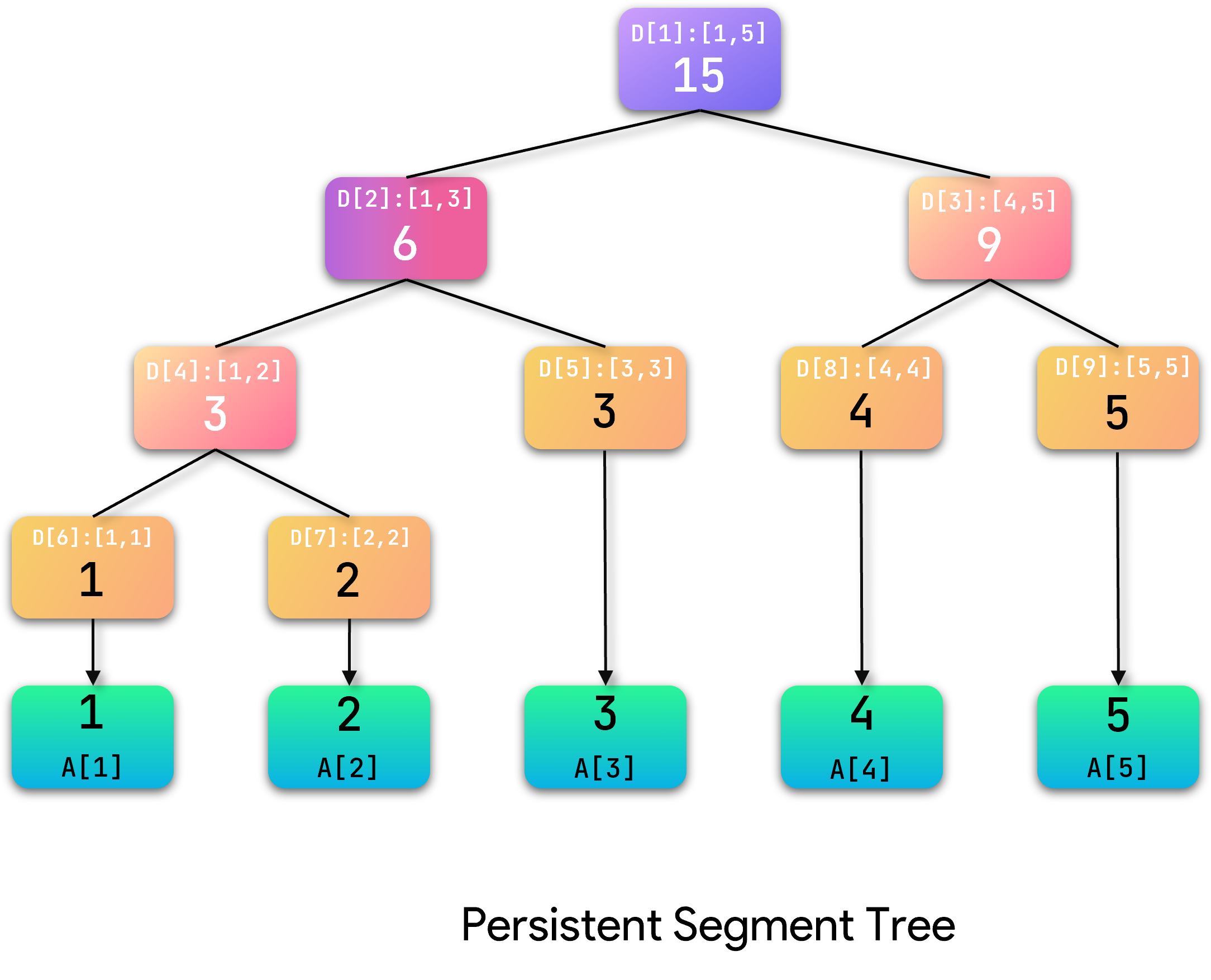
可以看到：不同于基础线段树，可持久化线段树的下标不再遵循堆的规律，这种建树方式我们称为动态开点。

结构体封装版：

#define ls(x) tree[x].ls
#define rs(s) tree[x].rs
#define val(x) tree[x].val
#define mark(x) tree[x].mark
struct node{
    int val, mark = INT_MIN;
    int ls, rs;
}tree[MAXN];

void build(int l = 1, int r = n, int p = 1){
    if(l == r) val(p) = a[l];
    else{
        ls(p) = ++cnt, rs(p) = ++cnt;
        int mid = (l + r) >> 1;
        build(l, mid, ls(p));
        build(mid + 1, r, rs(p));
        val(p) = val(ls(p)) + val(rs(p));
    }
}

建树完毕后，上述线段树已经静态化，后续的修改操作通过增加新节点来实现。

2.单点修改

假设现在要对 A [ 4 ] A[4] A[4]加 − 2 -2 −2，则操作步骤如下：

首先建立新根结点，更新根节点记录数组： r o o t [ f l a g ] = + + c n t root[flag] = ++cnt root[flag]=++cnt

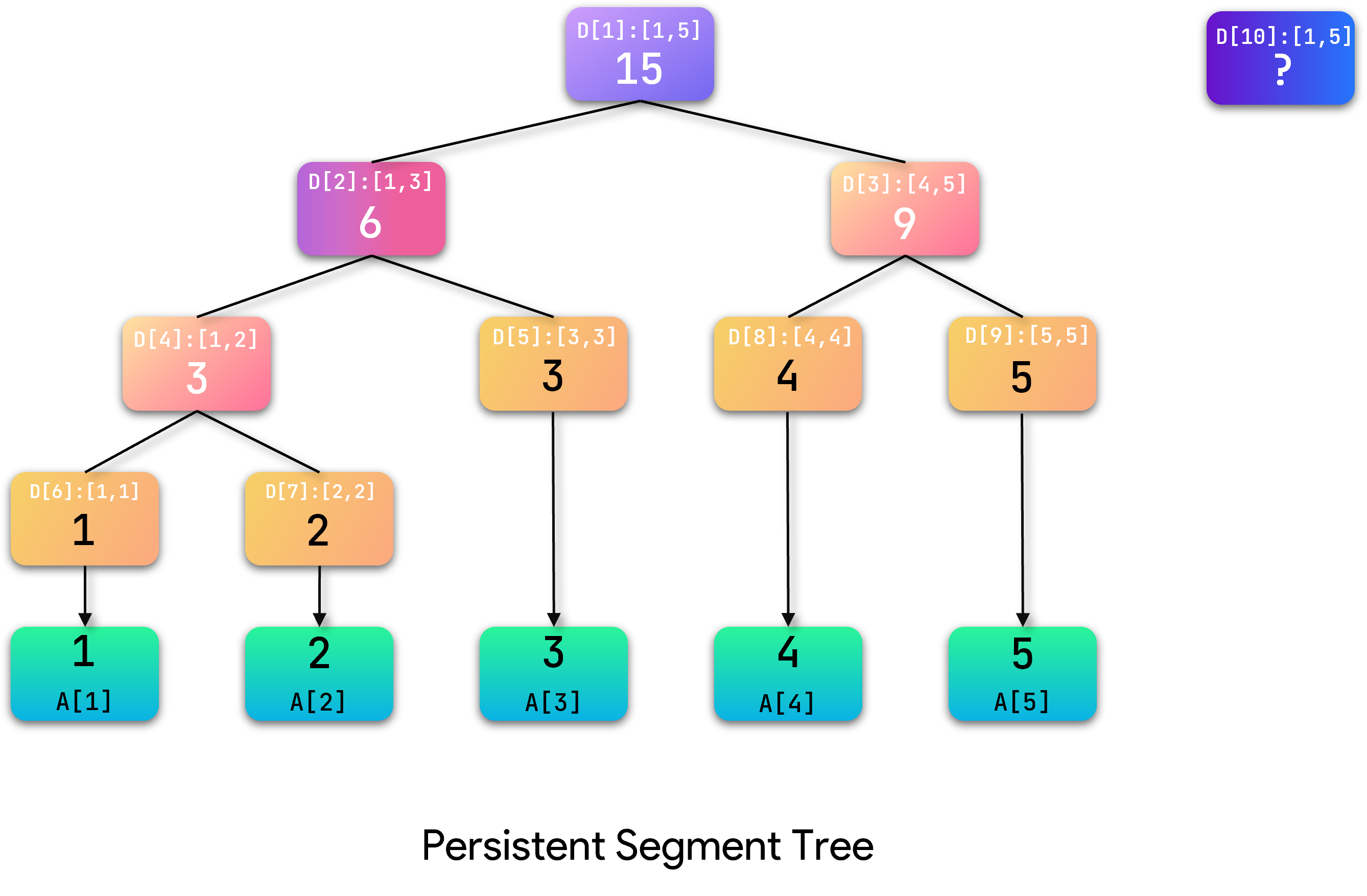
创建新节点后对其进行处理。由于我们要修改的元素 A [ 4 ] A[4] A[4]位于右子树，因此左子树部分保持不变，可以继续使用。因此将原左子树与新节点相连，同时新建右子节点。

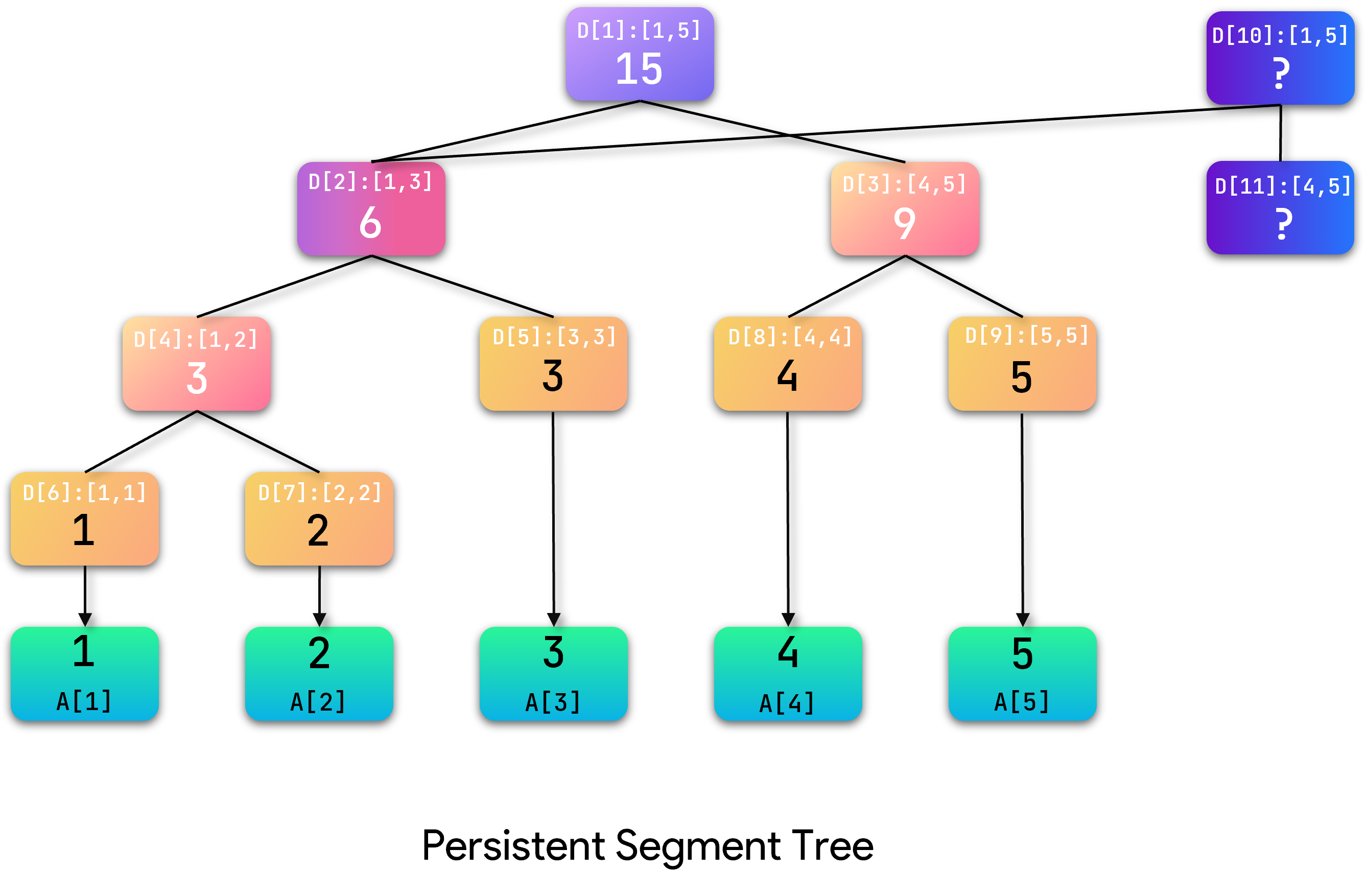
继续处理， A [ 4 ] A[4] A[4]位于当前结点左子树，右子树保持不变继续使用，因此新建左子节点，将原右子节点与新节点相连。

继续访问左子节点发现到达叶子结点，对原数据进行处理后再逐层回溯，更新路径上的结点值。

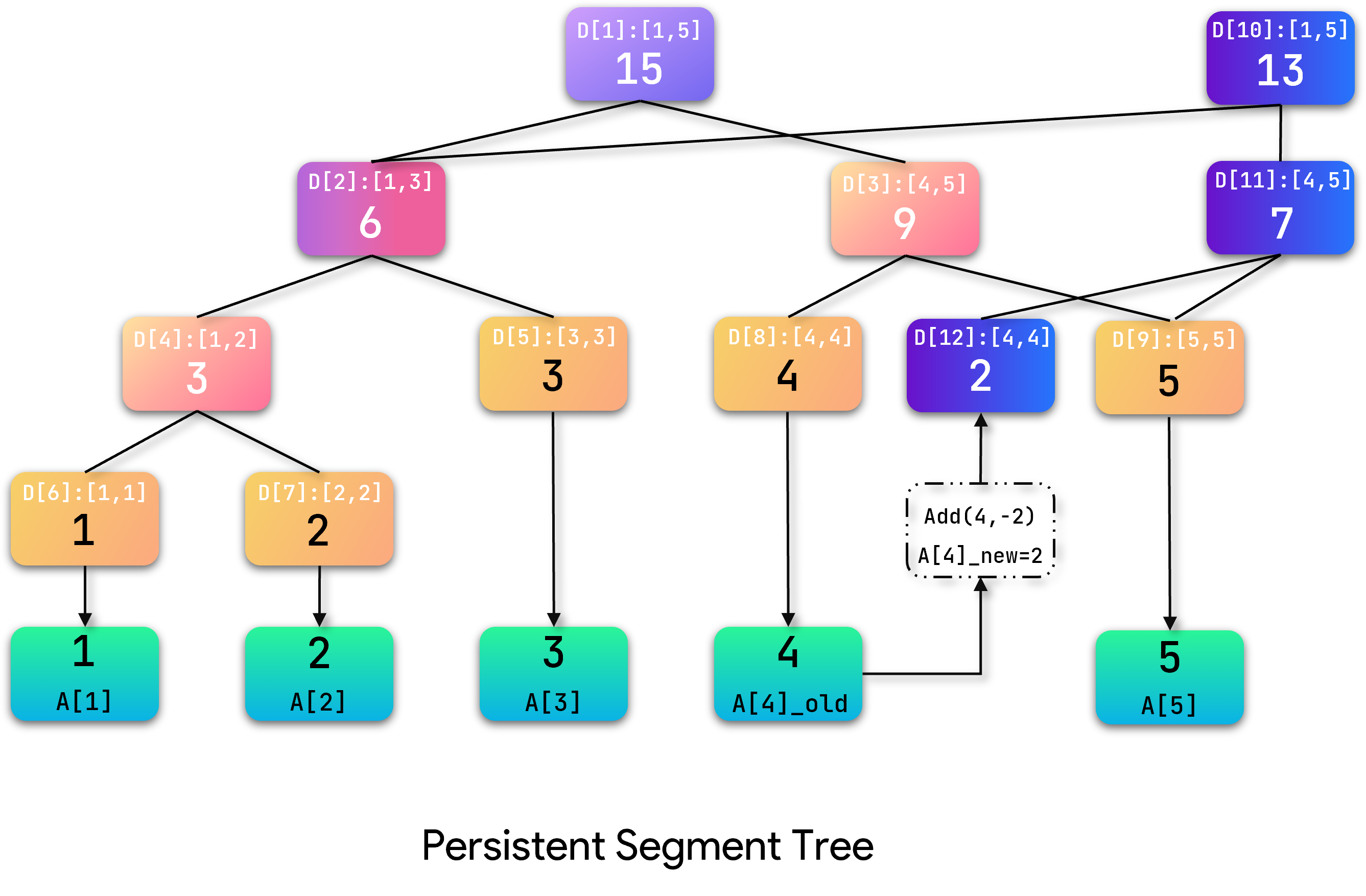
单点修改的操作到此结束。可以看到，对于最初版本的线段树，其任何数据未被改变。

void update(int x, int d, int p, int q, int cl = 1, int cr = n){
    if (cl == cr) val(q) = val(p) + d; // 给叶子节点赋值
    else{
        ls(q) = ls(p), rs(q) = rs(p); // 复制节点
        int mid = (cl + cr) / 2;
        if (x  r || cr = l && cr  r || cr = l && cr > 1;
        return query(l, r, ls(p), cl, mid, mk + mark(p)) + query(l, r, rs(p), mid + 1, cr, mk + mark(p)); // 带着标记传递
    }
}

对于 u p d a t e update update操作，其基本过程如下：

1. 首先对当前节点进行复制；
2. 判断：如果当前节点管辖区间合法，且是待修改区间的子集，那么对当前新的节点(复制后的节点)的标记执行加操作；
3. 如果不满足 2 2 2条件，则判断待修改区间是否由左子树管辖、是否由右子树管辖，如果是则复制节点，递归向左\右建点更新。

值得注意的是，由于缺少传递标记，因此由子节点给当前节点赋值可能会发生错误。

为了得到全包含的区间并计算真实长度，我们只需要定义区间为 [ m a x ( l , c l ) , m i n ( r , c r ) ] [max(l, cl), min(r, cr)] [max(l,cl),min(r,cr)]即可(保证其为带查询区间的子集)。

void update(int l, int r, int d, int p, int q, int cl = 1, int cr = n){
    ls(q) = ls(p), rs(q) = rs(p), mark(q) = mark(p); // 复制节点
    if (cl >= l && cr  cl) mark(q) += d;
    else{
        int mid = (cl + cr) >> 1;
        if (cl = l) ls(q) = ++cnt, update(l, r, d, ls(p), ls(q), cl, mid);// 提前进行判断，以免新建不必要的节点
        if (mid + 1 = l) rs(q) = ++cnt, update(l, r, d, rs(p), rs(q), mid + 1, cr);
            
    }
    val(q) = val(p) + (min(cr, r) - max(cl, l) + 1) * d; // 根据需要更新的区间长度计算当前节点的值
}

三、主席树

区别于一般的可持久化线段树，主席树是可持久化权值线段树。

下面简单介绍一下主席树的构造过程：

1.建立空树

void build(int l = 1, int r = n, int p = 1){
    val(p) = 0;
    if (l != r){
        ls(p) = ++cnt, rs(p) = ++cnt;
        int mid = (l + r) / 2;
        build(l, mid, ls(p));
        build(mid + 1, r, rs(p));
    }
}

2.区间离散化

int C[MAXN], L[MAXN], ori[MAXN];
void discretize(int A[], int n){
    memcpy(C, A, sizeof(int) * n);     // 复制
    sort(C, C + n);                    // 排序
    int l = unique(C, C + n) - C;      // 去重
    for (int i = 0; i