数据结构-ZKW线段树 详解

数据结构-ZKW线段树 详解 😊 | Powered By HeartFireY | ZKW Segment Tree 📕 | 需要的前导知识：基础线段树(Segment)、位运算 一、ZKW线段树简介

ZKW线段树是由清华大学张昆玮所创立的一种线段树储存结构，由于其基于非递归的实现方式以及精简的代码和较高的效率而闻名。甚至，ZKW线段树能够可持久化。

我们从算法的角度对基础线段树进行分析：其实线段树算法本身的本质仍是统计。因此我们可以从统计的角度入手对线段树进行分析：线段树是将一个个数 轴划分为区间进行处理的，因此我们面对的往往是一系列的离散量，这导致了我们在使用时的线段树单纯的退化为一棵"点树"(即最底层的线段树只包含一个点)。基于这一点可以入手对线段树进行优化

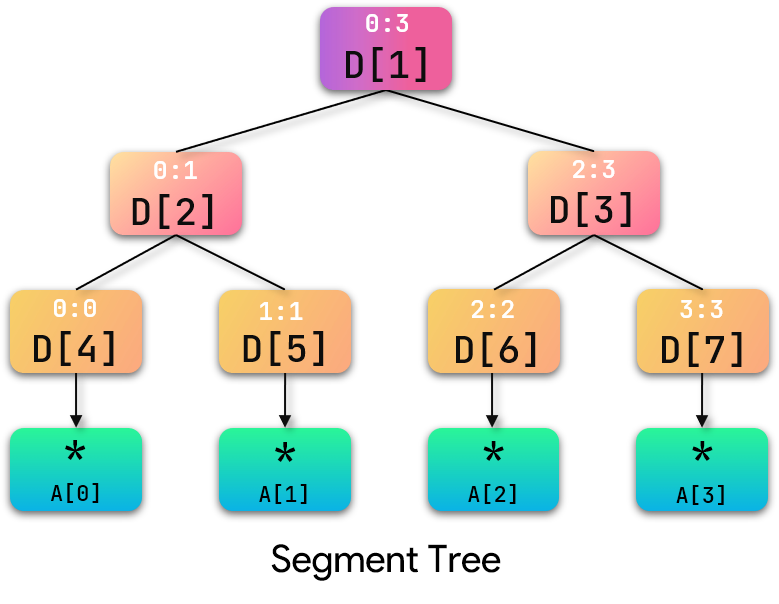
二、ZKW线段树的构造原理

首先，我们忽略线段树中的数据，从线段树的框架结构入手进行分析：如图所示是一颗采用堆式储存的基本线段树：

我们将节点编号转换为二进制：

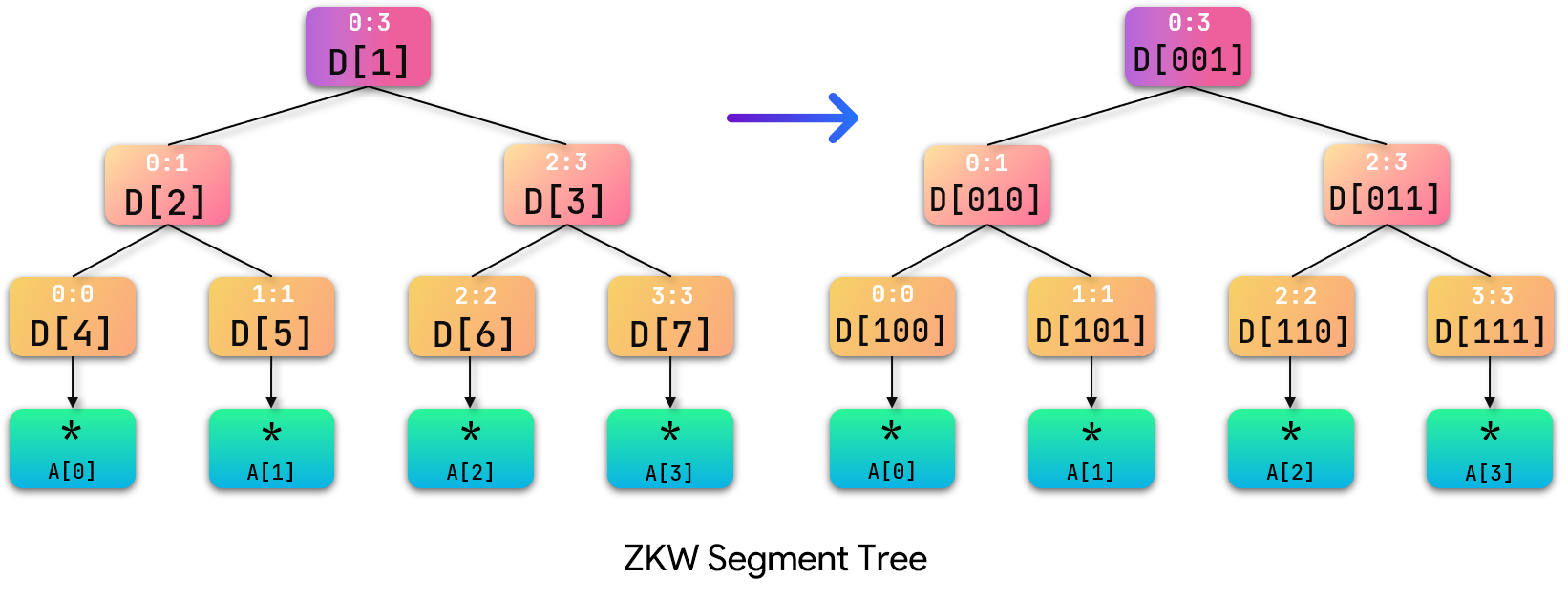
观察转为二进制后的结点规律：在基础线段树的学习中，我们知道对于任意结点 x x x，其左子节点为 x < < 1 x =1；

循环执行 2 − 3 2-3 2−3的步骤，直到 l l l和 r r r同为兄弟结点(此时不终止会导致重复计算)

如何判断是否为左子节点？我们很容易观察到左右子节点共同的特征：左子节点最低位为 0 0 0，右子节点最低位为 1 1 1，那么我们可以通过以下操作的真值判断左右子节点： 判 断 左 子 节 点 ： ∼ l   &   1 判 断 右 子 节 点 ：      r   &   1 判断左子节点：\sim l\ \&\ 1\\ 判断右子节点：\ \ \ \ r\ \&\ 1\\ 判断左子节点：∼l & 1判断右子节点：    r & 1 对于取兄弟结点的值则可以通过与 1 1 1异或求得：

左 子 节 点 求 兄 弟 结 点 ： l   x o r   1 右 子 节 点 求 兄 弟 结 点 ： r   x o r   1 左子节点求兄弟结点：l\ xor\ 1\\ 右子节点求兄弟结点：r\ xor\ 1\\ 左子节点求兄弟结点：l xor 1右子节点求兄弟结点：r xor 1

建立在上述操作的基础上，我们可以实现区间查询：

1. 维护区间和

   inline int get_sum(int l, int r, int ans = 0){
       for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1){
           if (~l & 1) ans += sum[l ^ 1];
           if (r & 1)  ans += sum[r ^ 1];
       } return ans;
   }
   

2. 维护区间最小值

   int get_min(int l, int r, int LL = 0, int RR = 0){
       for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1){
           LL += minn[l], RR += minn[r];
           if (~l & 1) LL = min(LL, minn[l ^ 1]);
           if (r & 1) RR = min(RR, minn[r ^ 1]);
       }
       int res = min(LL, RR);
       while (l) res += maxx[l >>= 1]; return res;
   }
   

3. 维护区间最大值

   int get_max(int l, int r, int LL = 0, int RR = 0){
       for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1){
           LL += maxx[l], RR += maxx[r];
           if (~l & 1) LL = max(LL, maxx[l ^ 1]);
           if (r & 1) RR = max(RR, maxx[r ^ 1]);
       }
       int res = max(LL, RR);
       while (l) res += maxx[l >>= 1]; return res;
   }
   

   ！注意：求最大值最小值不要忘记最后的统计步骤(差分还原)

5.区间修改

如何进行区间修改/更新？这个过程跟查询的思路是十分相似的，我们首先给出区间修改的思路：

1. 闭区间改开区间：需要让左端点 − 1 -1 −1，右端点 + 1 +1 +1；

2. 判断：当前区间左端点是否为左儿子，如果是则兄弟结点更新；

   判断：当前区间右端点是否为右儿子，如果是则兄弟结点更新；

3. 端点变量处理操作： l > > = 1 , r > > = 1 l >>= 1, r>>= 1 l>>=1,r>>=1；

4. 循环执行 2 − 3 2-3 2−3的步骤，直到 l l l和 r r r同为兄弟结点(此时不终止会导致重复计算)

根据上述过程可以得出代码(与查询是比较相似的)：

1. 维护区间和

   //这里有点问题，太晚了改天再改
   inline void update_part(int l, int r, ll v){
       for (l += m - 1, r += m + 1; l ^ r ^ 1; l >>= 1, r >>= 1, len = 1] += v;
   }
   

2. 维护区间最小值

   inline void update_part(int l, int r, int v, int A = 0){
       for(l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1){
           if (~l & 1) minn[l ^ 1] += v;
           if (r & 1) minn[r ^ 1] += v;
           A = min(minn[l], minn[l ^ 1]); minn[l] -= A, minn[l ^ 1] -= A, minn[l >> 1] += A;
           A = min(minn[r], minn[r ^ 1]); minn[r] -= A, minn[r ^ 1] -= A, minn[r >> 1] += A;
       }
       while(l) A = min(minn[l], minn[l ^ 1]), minn[l] -= A, minn[l ^ 1] -= A, minn[l >>= 1] += A;
   }
   

3. 维护区间最大值

   inline void update_part(int l, int r, int v, int A = 0){
       for(l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1){
           if (~l & 1) maxx[l ^ 1] += v;
           if (r & 1) maxx[r ^ 1] += v;
           A = min(maxx[l], maxx[l ^ 1]); maxx[l] -= A, maxx[l ^ 1] -= A, maxx[l >> 1] += A;
           A = min(maxx[r], maxx[r ^ 1]); maxx[r] -= A, maxx[r ^ 1] -= A, maxx[r >> 1] += A;
       }
       while(l) A = min(maxx[l], maxx[l ^ 1]), maxx[l] -= A, maxx[l ^ 1] -= A, maxx[l >>= 1] += A;
   }
   

四、Lazy标记 1. p u s h d o w n 、 p u s h u p pushdown、pushup pushdown、pushup类

ZKW线段树同样支持Lazy标记，也支持标记上下传。注意，一般不用这个方法，可以直接跳到标记永久化。

这里暂时没详细研究，先参考dalao博客放一个思路：

那么ZKW线段树中的Lazy标记是如何实现的呢？首先我们回到区间修改这个操作–大致的框架如下：

void update_part(int l, int r){
    for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1, updata(l), updata(r)){
        if (~l & 1) ... 
        if (r & 1)...
    }
    l >>= 1;
    while (l) updata(l), l >>= 1;
}

如果要实现 p u s h d o w n pushdown pushdown操作，只需额外添加一个 p u s h push push函数，其实就是用栈模拟基础线段树的标记下传操作。

void push(int x){
    int top = 0;
    while (x) sta[++top] = x, x >>= 1;
    while (top > 1) pushdown(sta[top--]);
}

将区间修改改为：

void update_part(int l, int r){
    for (l = l + m - 1, r = r + m + 1, push(l), push(r); l ^ r ^ 1; l >>= 1, r >>= 1, update(l), update(r)){
        if (~l & 1) ... 
        if (r & 1)...
    }
    l >>= 1;
    while (l) updata(l), l >>= 1;
}

2.标记永久化

标记永久化相关的概念不再赘述，与基础线段树一样的用法。

标记永久化之后的区间查询操作：

void update_part(int l, int r, ll k) {
    int lnum = 0, rnum = 0, now = 1;
    //lnum 表示当前左端点走到的子树有多少个元素在修改区间内 (rnum与lnum对称)
    //now 表示当前端点走到的这一层有多少个叶子节点
    for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1; now = 1, r >>= 1) sum[l] += k * lnum, sum[r] += k * rnum;
}

标记永久化之后的区间修改

ll query(int l, int r) {
    int lnum = 0, rnum = 0, now = 1;
    long long ret = 0;
    for (l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1, now = 1, r >>= 1) ret += add[l] * lnum, ret += add[r] * rnum;
    return ret;
}