深度学习_算法工程师 6 万字总结算法面试中的深度学习基础问题

目录

前言

第一章 机器学习

1.Batch Normalization

2.VGG使用使用3*3卷积核的优势是什么？

3.逻辑斯蒂回归（LR, Logistic Regression)

3.1 模型简介

3.2 相关问题

4.卷积

4.1 反卷积

4.2 空洞卷积

5.交叉熵与softmax

5.1 数学原理

5.2 交叉熵不适用于回归问题

5.3 交叉熵与softmax

6. 激活函数的意义

6.1 Sigmoid

6.2 tanh

6.3 RELU

7. pooling有什么意义，和卷积有什么区别

8.泛化误差（过拟合）

9. LR相关

10. SVM

10.1. 基本原理、意义(4)

11. 约束优化问题的对偶问题

11.Dropout

12. 评价指标

12.1 准确率和召回率（虚警和漏报）

12.2 PR曲线与F1值

12.3 ROC曲线与AUC值

12.4 怎么形成曲线：分类阈值α的调整形成

12.5 PR和ROC曲线应用场景对比：

13.正则化L1,L2

13.1 什么是正则化

13.2 L1正则化

13.3 L2正则化

13.4 L1和L2正则化的区别

13.5 总结

13.6 稀疏与平滑

13.7 使用场景：

13.8 如何解决L1求导困难：坐标下降法

13.9 坐标下降法缺点：

14.权重初始化

15. 决策树

15.1 原理

15.2 ID3

15.4 CART决策树

15.5 剪枝处理o

15.6 连续值处理（回归树）

15.7 缺失值处理

15.8 多变量决策树

15.9 LR、决策树、SVM的选择与对比

16. Boosting vs Bagging

16.1 集成学习

16.2 Boosting

16.3 Bagging

16.4 从减小偏差和方差来解释Boosting和Bagging

16.5 随机森林(RF)

17.优化算法

17.1 梯度下降法的变形形式

17.2 自适应学习率的方法

18. 线性判别分析

19. 朴素贝叶斯

20. 梯度提升决策树GBDT/MART (Gradient Boosting Decision Tree)

21. KMeans

22. 牛顿法

23. 缺失值的处理

24. 模型评估中常用的验证方法

25. 主成分分析PCA

26. Softmax函数的特点和作用是什么

27. 样本不均衡

28. 损失函数

29. 贝叶斯决策论

30. 采样

前言

真的是千呼万唤始出来emmmm，去年春招(2020)结束写了篇面试的经验分享。在文中提到和小伙伴整理了算法岗面试时遇到的常见知识点及回答，本想着授人以渔，但没想到大家都看上了我家的 ！但因本人执行力不足，被大家催到现在才终于想着行动起来分享给大家，笔者在这里给各位读者一个大大的抱歉，求原谅呜呜~~相信今年参加秋招的小伙伴们一定都拿到理想的offer啦，明年准备找工作的小盆友如果觉得本文还有些用可以收藏哈。

由于篇幅限制，就先发出前半部分，后面等下回笔者得空哈~另外欢迎小伙伴们转发！转发！再转发呀！！

第一章 机器学习 1.Batch Normalization

背景：由于Internal Covariate Shift(Google)效应，即深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。也就是随是着网络加深，参数分布不断往激活函数两端移动(梯度变小)，导致反向传播出现梯度消失，收敛困难。

原理：可在每层的激活函数前，加入BN，将参数重新拉回0-1正态分布，加速收敛。(理想情况下，Normalize的均值和方差应当是整个数据集的，但为了简化计算，就采用了mini_batch的操作)

机器学习中的白化（eg.PCA）也可以起到规范化分布的作用，但是计算成本过高。

BN不是简单的归一化，还加入了一个y = γx+β的操作，用于保持模型的表达能力。否则相当于仅使用了激活函数的线性部分，会降低模型的表达能力。

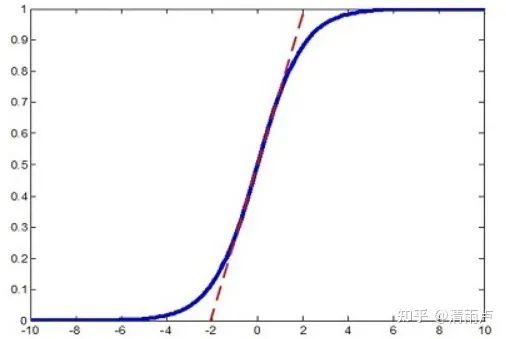
训练与测试：测试时均值和方差不再用每个mini-batch来替代，而是训练过程中每次都记录下每个batch的均值和方差，训练完成后计算整体均值和方差用于测试。

参考：

https://blog.csdn.net/sinat_33741547/article/details/87158830

https://blog.csdn.net/qq_34484472/article/details/77982224

https://zhuanlan.zhihu.com/p/33173246

BN对于Relu是否仍然有效？

有效，学习率稍微设置大一些，ReLU函数就会落入负区间(梯度为0)，神经元就会永远无法激活，导致dead relu问题。BN可以将数据分布拉回来。

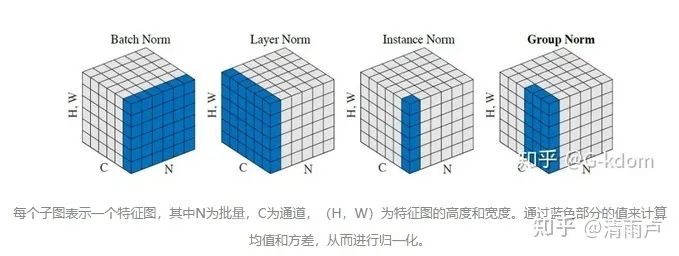
四种主流规范化方法

Batch Normalization(BN):纵向规范化 Layer Normalization(LN):横向规范化 对于单个样本 Weight Normalization(WN):参数规范化 对于参数 Cosine Normalization(CN):余弦规范化 同时考虑参数和x数据

多卡同步

• 原因

对于BN来说,用Batch的均值和方差来估计全局的均值和方差,但因此Batch越大越好.但一个卡的容量是有限的,有时可能batch过小,就起不到BN的归一化效果.

• 原理

利用多卡同步,单卡进行计算后,多卡之间通信计算出整体的均值和方差,用于BN计算, 等同于增大batch size 大小. 2次同步? 第一次同步获得全局均值,然后第二次计算全局方差

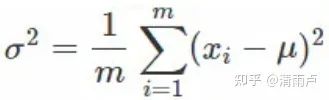
1次同步! 直接传递一次X和X2,就可直接计算出全局均值和方差.

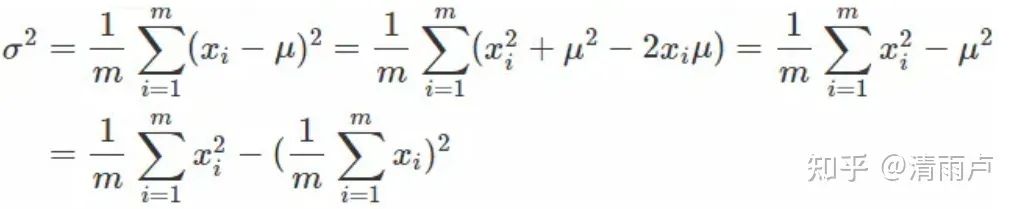
• 操作(pytorch)

注:

• 对于目标检测和分类而言,batch size 通常可以设置的比较大,因此不用多卡否则反而会因为卡间通讯,拖慢训练速度.

• 对于语义分割这种稠密的问题而言,分辨率越高效果越好,因此一张卡上容纳的batch size 比较小,需要多卡同步.

• 数据被可使用的GPU卡分割（通常是均分）,因此每张卡上BN层的batch size（批次大小）实际为:Batch Size/nGpu

2.VGG使用使用3*3卷积核的优势是什么？

2个3x3的卷积核串联和一个5x5的卷积核拥有相同的感受野，但是，2个3x3的卷积核拥有更少的参数，对于通道为1的5x5特征图得到通道为1的输出特征图，前者有3x3x2=18个参数，后者5x5=25个参数，其次，多个3x3的卷积核比一个较大的尺寸的卷积核加入了更多的非线性函数，增强了模型的非线性表达能力。

1x1卷积核的作用：改变通道数目，保持尺度不变情况下增强非线性表达能力，可以实现跨通道的信息交互。VGG：

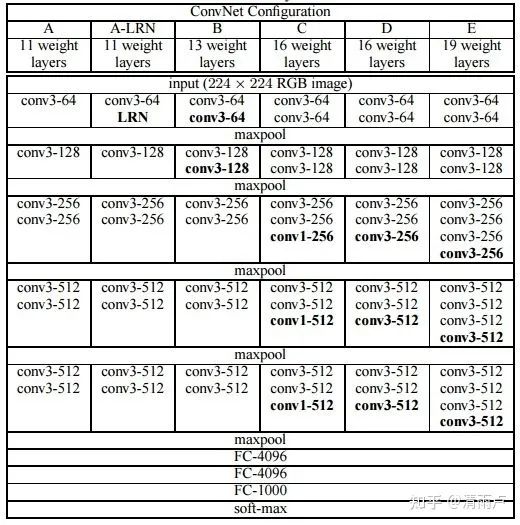
ResNet:

3.逻辑斯蒂回归（LR, Logistic Regression) 3.1 模型简介

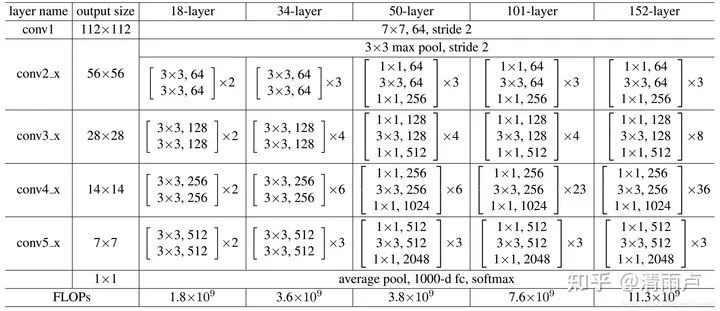
分布函数与概率密度函数：

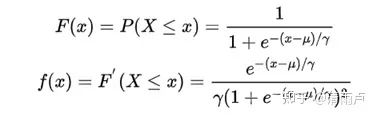
其中，μ表示位置参数，γ为形状参数。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在μ=0，γ=1的特殊形式。

损失函数：

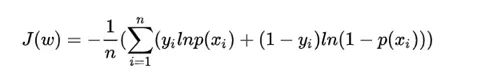
求解方法：1.随机梯度下降法 2.牛顿法

参考：https://zhuanlan.zhihu.com/p/74874291

3.2 相关问题

一、LR有什么特点？ 简单、容易欠拟合、值域为(0,1)、无穷阶连续可导。 各feature之间不需要满足条件独立假设，但各个feature的贡献独立计算

二、Sigmoid变化的理解？ a) sigmoid函数光滑，处处可导，导数还能用自己表示 b) sigmoid能把数据从负无穷到正无穷压缩到0，1之间，压缩掉了长尾，扩展了核心分辨率。 c) sigmoid在有观测误差的情况下最优的保证了输入信号的信息。

三、与SVM、线性回归等模型对比

参考：https://zhuanlan.zhihu.com/p/74874291

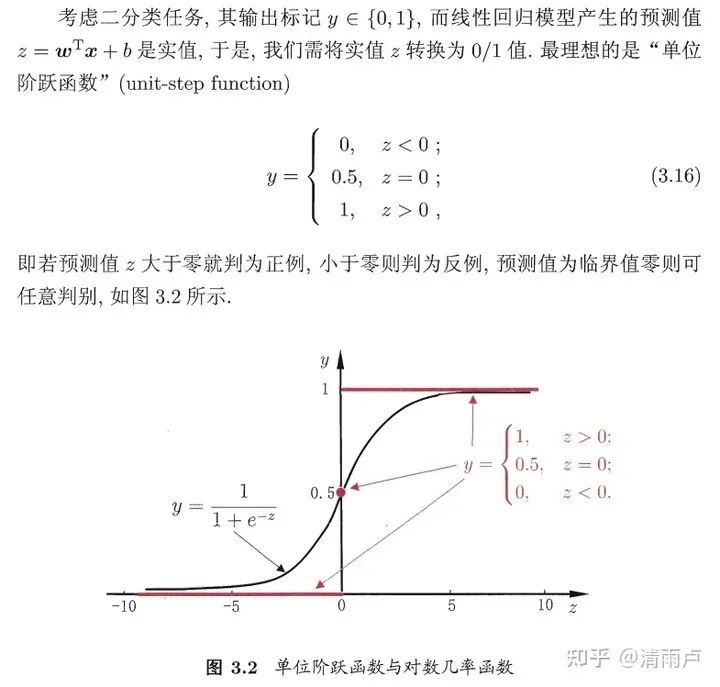
因为阶跃函数不连续，寻找替代函数如 sigmoid：

作变换可得到：

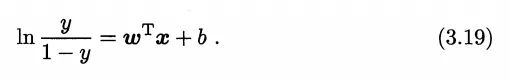
即用线性回归的结果去拟合事件发生几率(“几率”是事件发生与不发生的概率比值)的对数，这就是“对数几率回归”的名称来由，其名为回归，实际上是做分类任务。

为什么不用均方误差作为损失：

4.卷积

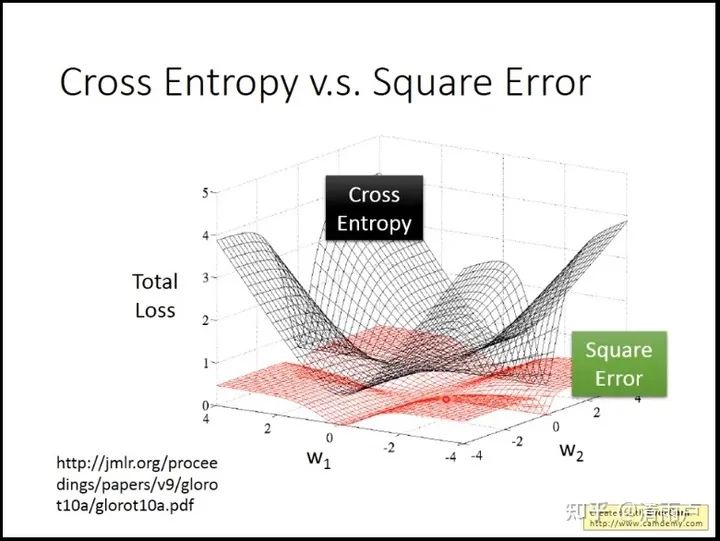
原理：卷积过程就是卷积核行列对称翻转后,在图像上滑动，并且依次相乘求和。(与滤波器不同的一点就是多了一个卷积核翻转的过程)。然后经过池化，激活后输入下一层。单个卷积层可以提取特征，当多个卷积叠加后即可逐步学习出更高语义的抽象特征。

这里提到了卷积，池化以及激活，那么池化以及激活的顺序如何考虑?

一般来说池化和激活的顺序对计算结果没有影响(其实是maxpooling无影响，但是如果用avgpooling的话，先后顺序还是会影响结果一点的)，但先池化可以减小接下来激活的计算量。

卷积核： 其中卷积核主要有两类，普通卷积核和1*1的卷积核。

普通卷积核同时改变图像的空间域和通道域，如下图所示，每个卷积核的通道数与输入相同，卷积后会得到一个通道为一的特征图，我们希望卷积后的通道数有几个，卷积核就有几个。

1*1卷积核，视野大小为单个特征位点,能够实现在空间域不改变的情况下实现通道域信息的交流,并且获得我们想要的通道数量(一般是降维)。

另外，1*1的卷积可以看作全连接。

参考:https://blog.csdn.net/amusi1994/article/details/81091145?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

4.1 反卷积

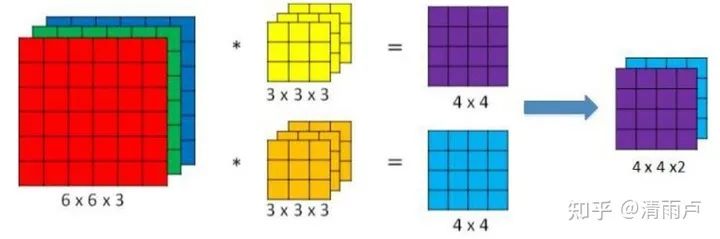
反卷积： 上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)，我们这里只讨论反卷积。

这里指的反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：反卷积是一种特殊的正向卷积，先按照一定的比例通过补0来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

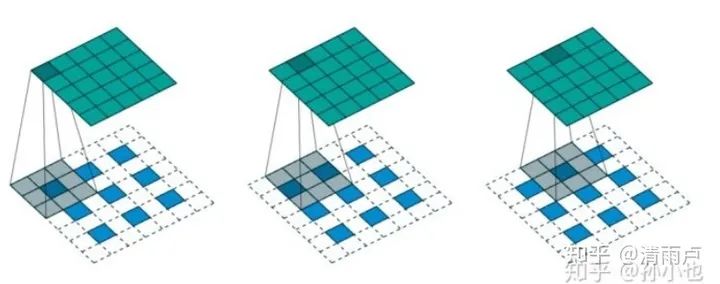
https://www.zhihu.com/question/48279880

4.2 空洞卷积

诞生背景

在图像分割领域，图像输入到CNN（典型的网络比如FCN[3]）中，FCN先像传统的CNN那样对图像做卷积再pooling，降低图像尺寸的同时增大感受野，但是由于图像分割预测是pixel-wise的输出，所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测，在先减小后增大尺寸的过程中，肯定有些信息损失掉了，如何避免？答案就是空洞卷积。

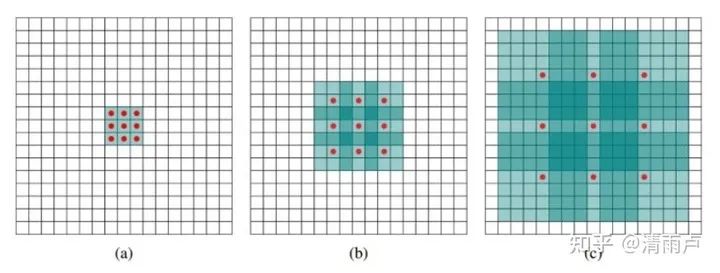
(a)图对应3x3的1-dilated conv，和普通的卷积操作一样，(b)图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个7x7的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为7x7，但是只有图中的9个点的权重不为0，其余都为0。(c)图是4-dilated conv操作

优点

dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者语音文本需要较长的sequence信息依赖的问题中，都能很好的应用dilated conv，比如图像分割、语音合成WaveNet、机器翻译ByteNet中。

潜在问题 1：The Gridding Effect

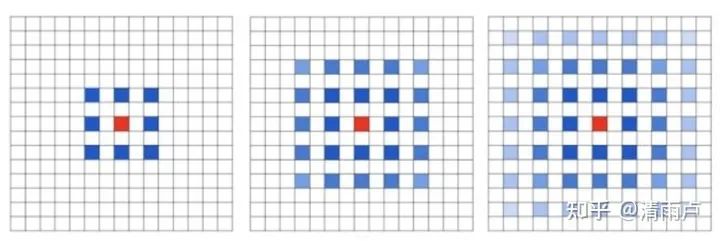
我们发现我们的 kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的。

潜在问题 2：Long-ranged information might be not relevant

我们从 dilated convolution 的设计背景来看就能推测出这样的设计是用来获取 long-ranged information。然而光采用大 dilation rate 的信息或许只对一些大物体分割有效果，而对小物体来说可能则有弊无利了。如何同时处理不同大小的物体的关系，则是设计好 dilated convolution 网络的关键。

通向标准化设计：Hybrid Dilated Convolution (HDC)

对于上个 section 里提到的几个问题，图森组的文章对其提出了较好的解决的方法。他们设计了一个称之为 HDC 的设计结构。

• 第一个特性是，叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积，依然会出现 gridding effect。

• 第二个特性是，我们将 dilation rate 设计成 锯齿状结构，例如 [1, 2, 5, 1, 2, 5] 循环结构。

• 第三个特性是，我们需要满足一下这个式子：

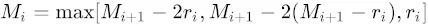
ri 是i层的dilation rate, Mi是i层的最大dilation rate, 那么假设总共有n层的话，默认 Mn = rn 。假设我们应用于 kernel 为 k x k 的话，我们的目标则是M2 c，其中c为常数。f′(x)=0，当|x|>c，其中c为常数。

一旦输入落入饱和区，f′(x)f′(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。

此外，sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

6.2 tanh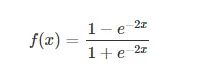

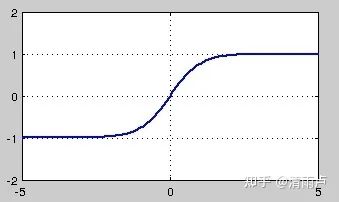
tanh也是一种非常常见的激活函数。与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。然而，从途中可以看出，tanh一样具有软饱和性，从而造成梯度消失。

tanh 的导数为 1-(tanh(x))2

6.3 RELU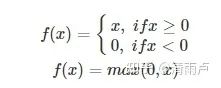

当x0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。

然而，随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。与sigmoid类似，ReLU的输出均值也大于0，偏移现象和 神经元死亡会共同影响网络的收敛性。针对在x3时，曲线趋于平稳。手肘法认 为拐点就是K的最佳值

K-means++算法：优化K-means“初始点”缺点 :

二分K-Means算法：

1. 将所有样本数据作为一个簇放到一个队列中。

2. 从队列中选择一个簇进行K-means算法划分，划分为两个子簇，并将子簇添加到队列中。

3. 循环迭代第二步操作，直到中止条件达到(聚簇数量、最小平方误差、迭代次数等)。

4. 队列中的簇就是最终的分类簇集合。

从队列中选择划分聚簇的规则一般有两种方式，分别如下：

1. 对所有簇计算误差和SSE(SSE也可以认为是距离函数的一种变种)，选择SSE最大的聚簇进行划分操作(优选这种策略)。

2. 选择样本数据量最多的簇进行划分操作

22. 牛顿法

xwn:牛顿法解决的问题：a,求解函数的根 b,求解函数极值

eg：求函数的根， 图像理解

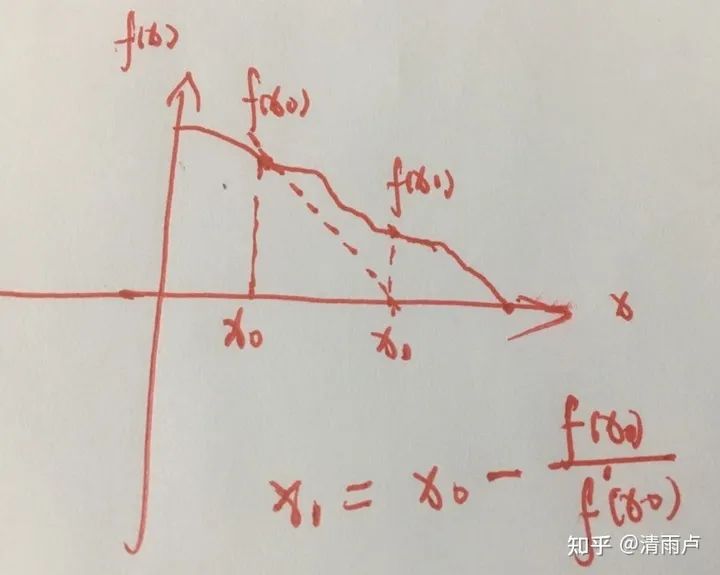
首先得明确，牛顿法是为了求解函数值为零的时候变量的取值问题的，具体地，当要求解 f(x)=0时，如果 f可导，那么将 f(x)展开：

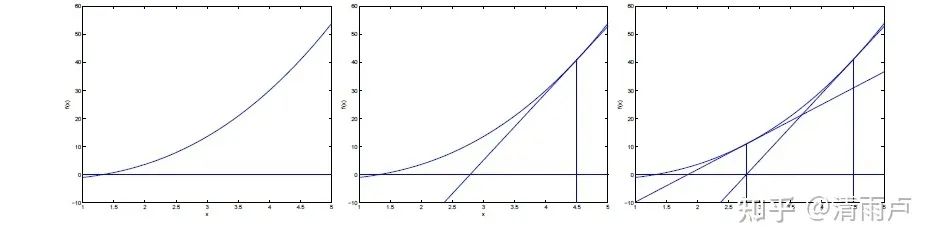
求局部最优点（极值点）

通过比较牛顿法和梯度下降法的迭代公式，可以发现两者极其相似。海森矩阵的逆就好比梯度下降法的学习率参数alpha。牛顿法收敛速度相比梯度下降法很快，而且由于海森矩阵的的逆在迭代中不断减小，起到逐渐缩小步长的效果。

海森矩阵：

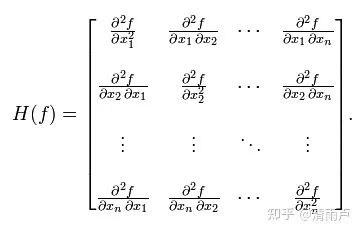
牛顿法的优缺点总结：

优点：二阶收敛，收敛速度快；

缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂，尤其是在高维情况下。(拟牛顿法就是以较低的计算代价求海森矩阵的近似逆矩阵)

参考： 

https://www.youtube.com/watch?v=FQN0-KHAgRw https://zhuanlan.zhihu.com/p/37588590 http://sofasofa.io/forum_main_post.php?postid=1000966

23. 缺失值的处理

缺失值的原因：

• 信息暂时无法获取。如商品售后评价、双十一的退货商品数量和价格等具有滞后效应。

• 信息被遗漏。可能是因为输入时认为不重要、忘记填写了或对数据理解错误而遗漏，也可能是由于数据采集设备的故障

• 获取这些信息的代价太大。如统计某校所有学生每个月的生活费，家庭实际收入等等。

• 有些对象的某个或某些属性是不可用的。如一个未婚者的配偶姓名、一个儿童的固定收入状况等

_缺失值较多：_直接舍弃该特征缺失值较少（b，如果取max，那么就直接取a，没有第二种可能。

但有的时候我们不想这样，因为这样会造成分值小的那个饥饿。所以我希望分值大的那一项经常取到，分值小的那一项也偶尔可以取到，那么我用softmax就可以了。

现在还是a和b，a>b，如果我们取按照softmax来计算取a和b的概率，那a的softmax值大于b的，所以a会经常取到，而b也会偶尔取到，概率跟它们本来的大小有关。所以说不是max，而是Softmax那各自的概率究竟是多少呢，我们下面就来具体看一下

定义：

1、计算与标注样本的差距

在神经网络的计算当中，我们经常需要计算按照神经网络的正向传播计算的分数S1，和按照正确标注计算的分数S2，之间的差距，计算Loss，才能应用反向传播。

Loss定义为交叉熵

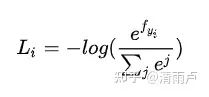
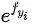
样本中正确的那个分类的对数值。

取log里面的值就是这组数据正确分类的Softmax值，它占的比重越大，这个样本的Loss也就越小，这种定义符合我们的要求。

2、计算上非常方便

当我们对分类的Loss进行改进的时候，我们要通过梯度下降，每次优化一个step大小的梯度。我们定义选到yi的概率是

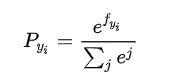
然后我们求Loss对每个权重矩阵的偏导，应用链式法则

27.样本不均衡

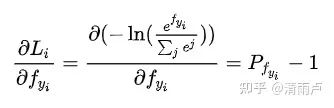
导致模型性能降低的本质原因

模型训练时优化的目标函数和人们在测试时的评价标准不同：

1. 分布：在训练时优化的是整个训练集（正负样本比例可能是1∶99）的正确率 而测试时可能想要模型在正样本和负样本上的平均正确率尽可能大（实际上是期望正负样本比例为 1∶1）

2. 权重（重要性）：训练时认为所有样本的贡献是相等的，而测试时假阳性样本（False Positive） 和伪阴性样本（False Negative）有着不同的代价

• 解决办法

• 基于数据

a）随机采样：欠采样(有放回)+过采样（放不放回都可以） 欠采样对少数样本进行多次复制，扩大了数据规模，但容易造成过拟合。

欠采样丢弃部分样本，有可能会丢失部分有用信息，导致模型只学到了整体模式的部分。

b)SMOTE算法(针对过采样）不再简单的复制样本，而是生成新样本，降低过拟

对少数类的数据集的每一个样本x,从其k近邻中随机选取一个样本y,在其连线上随机选取一点，作为新合成的样本。

根据采样倍率重复操作

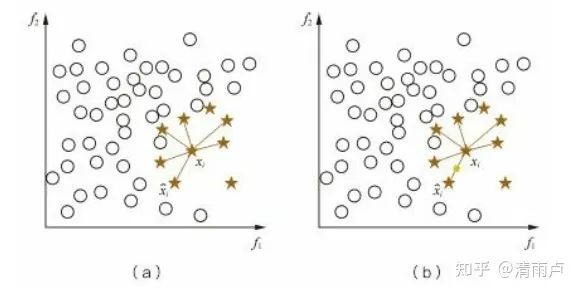
每个少数类样本合成相同数量的新样本，这可能会增大类间重叠度，并且会生成一些不能提供有益信息的样本 i）Borderline-SMOTE:只给那些处在分类边界上的少数类样本 合成新样本

ii)ADASYN: 给不同的少数类样本合成不同个数的新样本

iii）数据清理方法:进一步降低合成样本带来的类间重叠

数据扩充方法也是一种过采样，对少数类样本进行一些噪声扰动或变换（如图像数据集中对图片进行裁剪、翻转、旋转、加光照等）以构造出新的样本

c)Informed Undersampling(欠采样):解决数据丢失问题

i)easy ensemble 从多数类中随机抽取子集E,与所有少数类训练基分类器。重复操作后，基分类器融合

ii)Balance Cascade 从多数类中随机抽取子集E,与所有少数类训练基分类器。从多数类中剔除被分类正确的样本，继续重复操作融合基分类器。

基于算法

1. 改变损失函数，不同类别不同权重 ------不平衡

2. 转化为单类学习（one-class learning)---极度不平衡

3. 异常检测（anormaly detection)

28.损失函数

回归

• MSE loss／均方误差－－Ｌ２损失

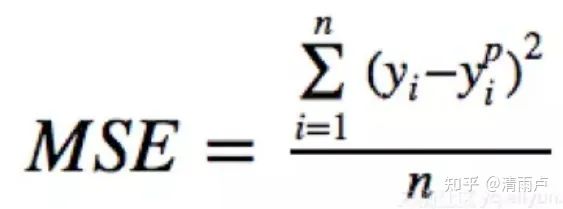
• MAE loss／平均绝对误差－－L１损失

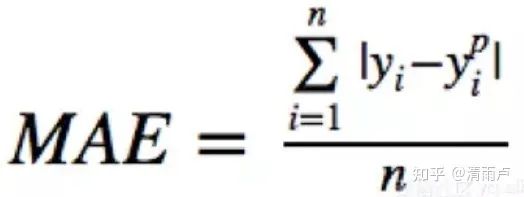
• MSE VS MAE

MSE易求解，但对异常值敏感， 得到观测值的均值 MAE对于异常值更加稳健， 得到观测值的中值

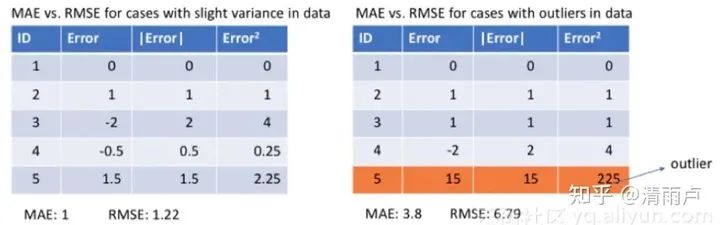
对于误差较大的异常样本，MSE损失远大于MAE，使用MSE的话，模型会给予异常值更大的权重，全力减小异常值造成的误差，导致模型整体表现下降。因此，训练数据中异常值较多时，MAE较好。

但MAE在极值点梯度会发生跃迁，即使很小的损失也会造成较大的误差，为解决这一问题，可以在极值附近动态减小学习率

总结：MAE对异常值更加鲁棒，但导数的不连续导致找最优解过程中低效

MSE对异常值敏感，但优化过程更加稳定和准确

问题：例如某个任务中90%的数据都符合目标值——150，而其余的10%数据取值则在0-30之间，那么利用MAE优化的模型将会得到150的预测值而忽略的剩下的10%（倾向于中值）；

而对于MSE来说由于异常值会带来很大的损失，将使得模型倾向于在0-30的方向取值。

Huber loss/平滑平均绝对误差

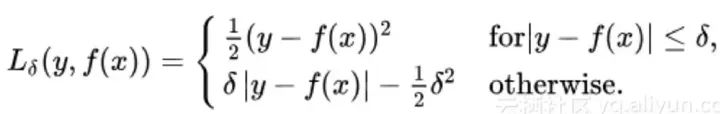
对异常值不敏感，且可微 使用超参数δ来调节这一误差的阈值。当δ趋向于0时它就退化成了MAE，而当δ趋向于无穷时则退化为了MSE

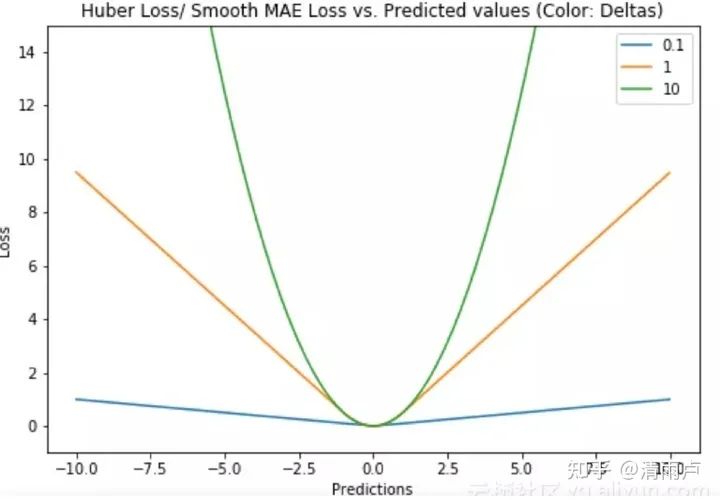
Log-Cosh loss

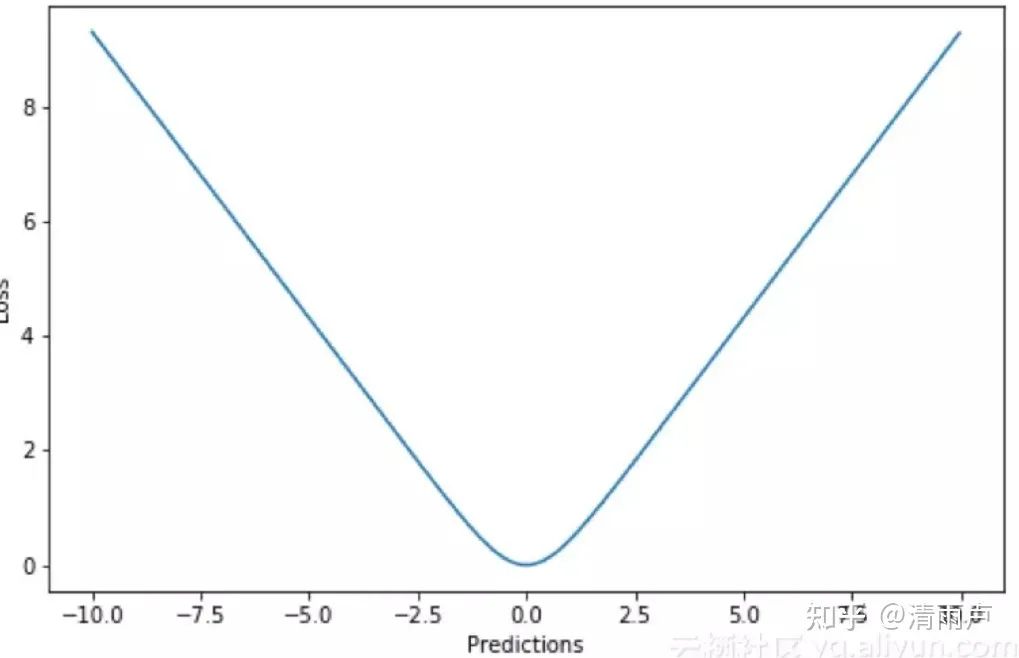
拥有Huber的所有优点，并且在每一个点都是二次可导的。二次可导在很多机器学习模型中是十分必要的

Quantile loss/分位数损失

参考：https://www.jianshu.com/p/b715888f079b

• 分类

• 0-1 loss（很少使用）

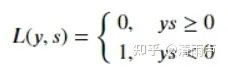
对每个错分类点都施以相同的惩罚 不连续、非凸、不可导，难以使用梯度优化算法

Cross Entropy Loss/交叉熵损失

Hinge Loss

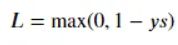
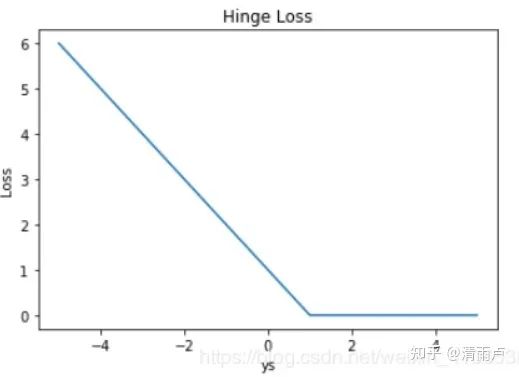
一般多用于支持向量机（SVM） ys > 1 的样本损失皆为 0，由此带来了稀疏解，使得 SVM 仅通过少量的支持向量就能确定最终超平面

Exponential loss/指数损失

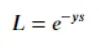
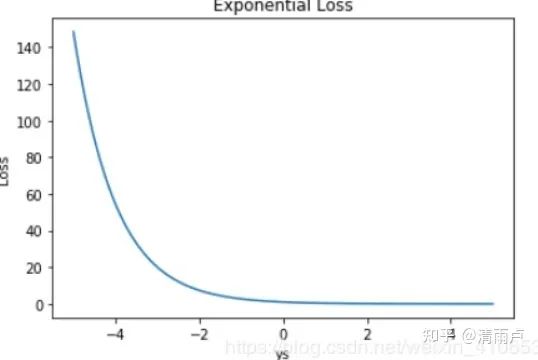
一般多用于AdaBoost 中。因为使用 Exponential Loss 能比较方便地利用加法模型推导出 AdaBoost算法。该损失函数对异常点较为敏感，相对于其他损失函数robust性较差

Modified Huber loss

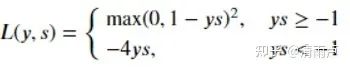
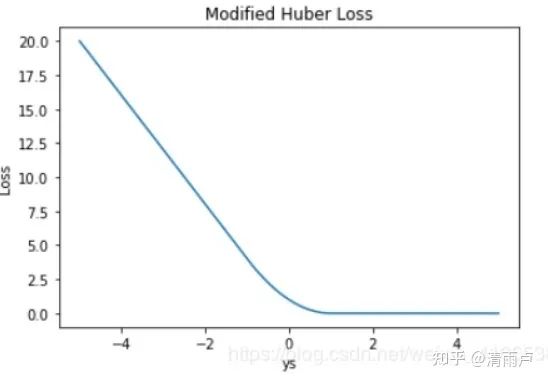
结合了 Hinge Loss 和 交叉熵 Loss 的优点。一方面能在 ys > 1 时产生稀疏解提高训练效率；另一方面对于 ys < −1 样本的惩罚以线性增加，这意味着受异常点的干扰较少

Softmax loss

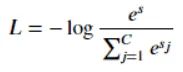
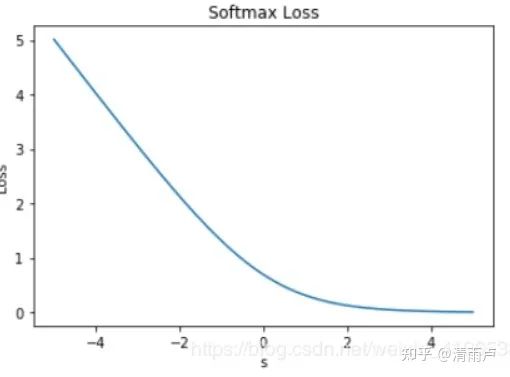
当 s >0 时，Softmax 趋向于零。Softmax 同样受异常点的干扰较小，多用于神经网络多分类问题中

注：相比 Exponential Loss，其它四个 Loss，包括 Softmax Loss，都对离群点有较好的“容忍性”，受异常点的干扰较小，模型较为健壮

参考：https://blog.csdn.net/weixin_41065383/article/details/89413819

focal loss

背景：

one-stage网络因为正负样本严重不均衡，且负样本中还有很多易区分的原因，精度一般低于two-stage 网络(two-stage 利用RPN网络，将正负样本控制在1：3左右）

原理：

1，解决正负样本不均衡问题：添加权重控制，增大少数类样本权重

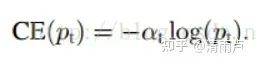
2，解决难易样本问题：Pt越大说明该样本易区分，应当降低容易区分样本的权重。也就是说希望增加一个系数，概率越大的样本，权重系数越小。 另，为提高可控性，引入系数γ

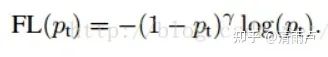
综合：两个参数α和γ协调来控制，本文作者采用α=0.25，γ=2效果最好

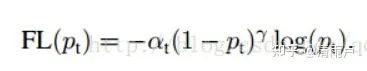
参考：https://blog.csdn.net/wfei101/article/details/79477303

29.贝叶斯决策论

概率框架下实施决策的基本方法

以多分类举例： 共 N 种类别，λij 为将 j 类样本误分类为 i 类样本所产生的损失。

那么，给定样本 x，将其分类为 i 类样本所产生的期望损失为：

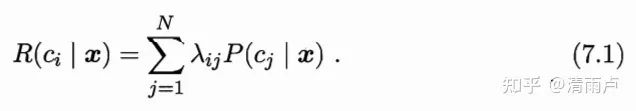
任务目标为找到分类器 h:X→Y ，使总体损失最小：

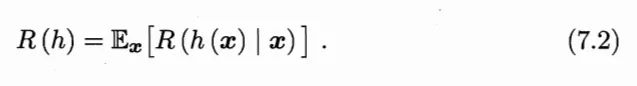
最好的 h 显然是对每个样本 x，都选择期望损失最小的类别：

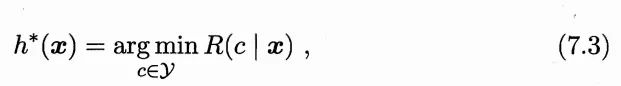
h* 就叫贝叶斯最优分类器，R(h*)叫贝叶斯风险，1-R(h*) 是分类器所能达到的最优性能，即通过机器学习所能产生的模型精度的理论上限。

比如，目标是最小化误分类率，那么：

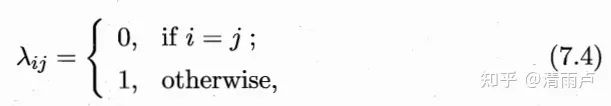
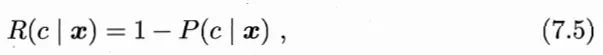
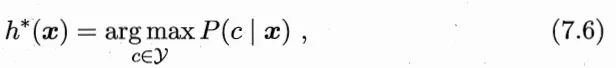
判别式 vs 生成式

两者的本质区别在于建模对象不同。

• 判别式

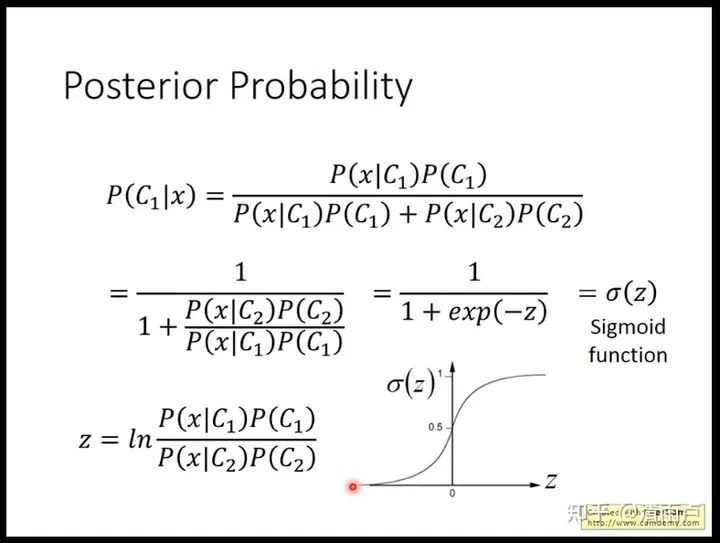
直接对 P(c|x) 建模：给定 x，使用模型预测其类别 c，通过各种方法来选择最好的模型。

• 生成式

对 P(c,x) 建模，再计算 P(c|x)：

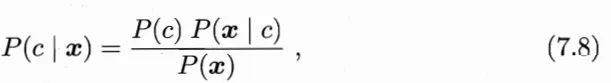
P(c)好得，P(x)无所谓，重点在如何获取 P(x|c).

极大似然估计

假设 P(x|c) 满足某种分布(分布参数为 θ)，再用极大似然估计找出 θ.

朴素贝叶斯

假设 x 中所有属性相互独立：

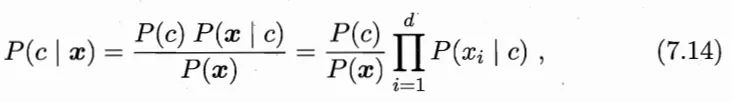
生成式模型理解 LR：

常见的判别式与生成式模型：

判别式：线性回归、逻辑回归、线性判别分析、SVM、神经网络

生成式：隐马尔科夫模型HMM、朴素贝叶斯、高斯混合模型GMM、LDA、KNN

优缺点：

1. 生成式模型最终得到的错误率会比判别式模型高，但是收敛所需的训练样本数会比较少。

2. 生成式模型更容易拟合，比如在朴素贝叶斯中只需要计数即可，而判别式模型通常都需要解决凸优化问题。

3. 生成式模型可以更好地利用无标签数据。

4. 生成式模型可以用来生成样本 x.

5. 生成式模型可以用来检测异常值。

30.采样

实现均匀分布的随机数生成器

计算机程序都是确定性的，因此并不能产生真正意义上的完全均匀分布随机数，只能产生伪随机数。

计算机 的存储和计算单元只能处理离散状态值，因此也不能产生连续均匀分布随机数，只能通过离散分布来逼近连续分布（用很大的离散空间来提供足够的精度）

线性同余法：根据当前生成的随机数xt来进行适当变换，进而产生下一次的随机数xt+1 。初始值x0称为随机种子

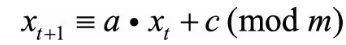
得到的是区间[0,m−1]上的随机整数，如果想要得到区间[0,1]上的连续均匀分布随机数，用xt除以m即可。

实际上对于特定的种子，很多数无法取到，循环周期基本达不到m。进行多次操作，得到的随机数序列会进入循环周期gcc中的设置

种子seed应该是随机选取的，可以将时间戳作为种子。