Polygon zkEVM哈希状态机——Keccak-256和Poseidon

1. 引言

前序博客有：

• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM语法

Polygon zkEVM中主要使用了2类哈希函数：

• 1）Keccak-256哈希函数：可参看SHA-3 and The Hash Function Keccak。【因EVM Storage使用Keccak-256哈希函数来构建Merkle树。】【zkASM相关指令有：HASHK、HASHKLEN、HASHKDIGEST。】
• 2）Poseidon哈希函数：可参看POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems 学习笔记。【zkEVM内部使用Poseidon哈希函数，以降低证明复杂度。】【zkASM相关指令有：HASHP、HASHPLEN、HASHPDIGEST。】

这2种哈希函数都采用了Sponge construction。 所谓Sponge construction，是一种迭代结构，用于构建函数： F : Z ∗ → Z l F: \mathbb{Z}^* \to \mathbb{Z}^l F:Z∗→Zl 即基于可变长度的input，得到特定长度的输出。核心为a fixed-length permutation： f : Z b → Z b f: \mathbb{Z}^b \to \mathbb{Z}^b f:Zb→Zb 该permutation对a fixed number b b b of bits进行运算。 其中 b b b称为width， f f f函数所持续转换的 b b b bits数组称为state。可将该state array切分为2段，分别具有 r r r bits和 c c cbits，其中 r r r 称为bitrate（或rate）， c c c称为capacity。这样切分的目的后续将介绍。

Sponge construction的基本工作原理为：

• 1）初始化阶段：首先，需根据可逆填充规则对输入字符串进行填充，使得填充后的字符串长度可被 r r r整除，然后将输入字符串按 r r r bits切分为多个blocks。同时，将state中的 b b b bits都初始化为0。
• 2）Absorbing阶段：在该阶段，将input blocks的 r r r bits 与 state中的前 r r r bits 进行异或操作，与permutation函数 f f f的应用交错进行。直到处理完所有的 r r r bits input blocks。注意，最终的 c c c bits对应为不从外部吸收任何输入的capacity值。
• 3）Squeezing阶段：在该阶段中，state的前 r r r bits作为output blocks，与permutation函数 f f f的应用交错执行。output blocks的数量由用户选择。注意，最终的 c c c bits对应为capacity值，在该阶段永远不输出。实际上，若输出值大于指定的长度，可简单裁剪即可。

具体如下图所示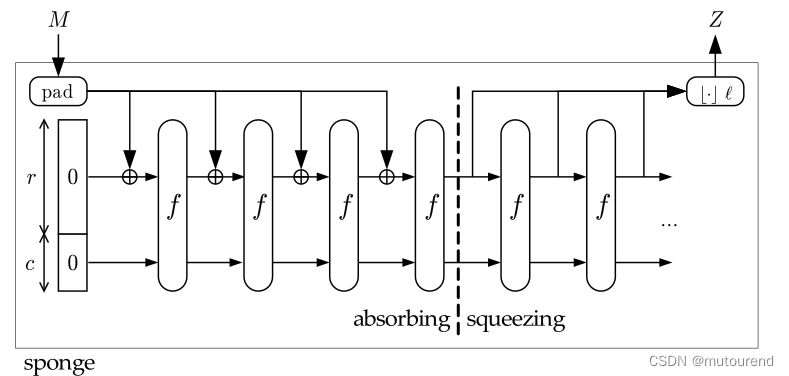： 要唯一确定Sponge construction所需的参数有：

• 1）fixed-length permutation f f f；
• 2）填充规则pad；
• 3）rate value r r r。

2. Polygon zkEVM中的Keccak-256哈希函数

EVM所使用的KECCAK-256哈希函数，采用了KECCAK[512] sponge construction。 首先定义KECCAK[c] sponge construction：【 c c c表示capacity】

• width为： 1600 1600 1600 bits
• rate为： 1600 − c 1600-c 1600−c bits

对于KECCAK[512]，rate为1088 bits（等价为136 bytes），capacity为512 bits（等价为64 bytes）。

根据 NIST SHA-3 Stanard中： 可知，KECCAK[c]使用的permutation为KECCAK-p[1600,24]。 自此，已完成了对rate r r r 和 fixed-length permutation f f f的定义。为完整定义具体的哈希函数，最后需指定相应的填充规则。

KECCAK[c]使用的填充规则为pad10*1： 若定义 j = ( − m − 2 ) m o d    r j=(-m-2)\mod r j=(−m−2)modr 其中 m m m为原始input的bit length，然后对原始input进行填充： P = 1 ∣ ∣ 0 j ∣ ∣ 1. P = 1 \mid\mid 0^j \mid\mid 1. P=1∣∣0j∣∣1.

自此，已知input bit string M M M 和 output length d d d，KECCAK[c](M,d)会根据之前的sponge construction描述，生成 d d d bit string。

注意，Polygon zkEVM的KECCAK-256并不遵循FIPS-202标准（即并不遵循SHA-3标准）。根据NIST规范，SHA3 padding应为： SHA3-256 ( M ) = KECCAK [ 512 ] ( M ∣ ∣ 01 , 256 ) . \text{SHA3-256}(M) = \text{KECCAK}[512](M \mid\mid 01, 256). SHA3-256(M)=KECCAK[512](M∣∣01,256).

差别在于，原始的KECCAK规范中并没有在 原始消息之后额外附加01 bits。

Polygon zkEVM中实现的KECCAK-256哈希函数约束见zkevm-proverjs/pil/：

• padding_kk.pil
• padding_kkbit.pil
• norm_gate9.pil
• keccak.pil
• nine2one.pil

相关测试用例见：

• zkevm-proverjs/test/sm/sm_padding_kk_test.js
• zkevm-proverjs/test/counters/keccak.js

2.1 KECCAK-256中的pad10*1填充约束

根据 NIST SHA-3 Stanard 可知，pad10*1为KECCAK的multi-rate填充规则，表示填充内容为一个1、后续为一组0（可能也没有0）、然后最后一个1。

pad10*1 填充算法为：【最少填充2个bit（即开始一个1和最后一个1）；最多填充 x + 1 x+1 x+1个bit。】 Polygon zkEVM中实现的pad10*1约束见zkevm-proverjs/pil/：

• padding_kk.pil

2.2 Keccak-256 zkASM示例

见zkevm-proverjs中的keccak.zkasm例子为：

start:

        STEP => A
        0 :ASSERT

        ; to verify that there are no correlations between counters
        0 => A
        CNT_ARITH :ASSERT
        CNT_BINARY :ASSERT
        CNT_MEM_ALIGN :ASSERT
        CNT_KECCAK_F :ASSERT
        CNT_POSEIDON_G :ASSERT
        CNT_PADDING_PG :ASSERT

        ; TEST 135 bytes => counter increase 1 => total = 1
		; incCounter=Math.ceil((len+1) / 136)，向上取整。total=0
        0 => E
        0 => HASHPOS ;将位置重置为0
        32 => D ;设置每个HASHK结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D=32*4=128
        7 => D ;设置每个HASHK结果为7 byte
        0x5E1268E5B2A8DCn :HASHK(E) ; len=len+D=135

        135            :HASHKLEN(E) ; len
        $ => A         :HASHKDIGEST(E) 

        1 => A ; incCounter=Math.ceil((135+1)/136)=1。total=total+incCounter=1
        CNT_KECCAK_F   :ASSERT ;  cntKeccakf计数单位为incCounter，实际即为total值。

        ; TEST 136 bytes => counter increase 2 => total = 3

        E + 1 => E
        0 => HASHPOS ;将位置重置为0
        32 => D ;设置每个HASHK结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D=32*4=128
        8 => D ;设置每个HASHK结果为8 byte
        0x5E1268E5B2A8DC1Dn :HASHK(E)  ; len=len+D=128+8=136

        136            :HASHKLEN(E) ; len
        $ => A         :HASHKDIGEST(E) 

        3 => A ; incCounter=Math.ceil((136+1)/136)=2，total=total+incCounter=3
        CNT_KECCAK_F   :ASSERT ;  cntKeccakf计数单位为incCounter，实际即为total值。

        ; TEST 271 bytes => counter increase 2 => total = 5

        E + 1 => E
        0 => HASHPOS ;将位置重置为0
        32 => D ;设置每个HASHK结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D=32*8=256
        ; 256

        15 => D ;设置每个HASHK结果为15 byte
        0x5E1268E5B2A8DC1D0BB047386FC227n :HASHK(E) ; len=len+D=256+15=271

        271            :HASHKLEN(E)
        $ => A         :HASHKDIGEST(E)

        5 => A  ; incCounter=Math.ceil((271+1)/136)=2，total=total+incCounter=5
        CNT_KECCAK_F   :ASSERT ;  cntKeccakf计数单位为incCounter，实际即为total值。


        ; TEST 272 bytes => counter increase 3 => total = 8

        E + 1 => E
        0 => HASHPOS ;将位置重置为0
        32 => D ;设置每个HASHK结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHK(E) ; len=len+D=32*8=256
        ; 256

        16 => D ;设置每个HASHK结果为16 byte
        0x5E1268E5B2A8DC1D0BB047386FC227FAn :HASHK(E) ; len=len+D=256+16=272

        272            :HASHKLEN(E)
        $ => A         :HASHKDIGEST(E)

        8 => A  ; incCounter=Math.ceil((272+1)/136)=3，total=total+incCounter=8
        CNT_KECCAK_F   :ASSERT ;  cntKeccakf计数单位为incCounter，实际即为total值。

        ; to verify that there are no correlations between counters
        0 => A
        CNT_ARITH :ASSERT
        CNT_BINARY :ASSERT
        CNT_MEM_ALIGN :ASSERT
        CNT_POSEIDON_G :ASSERT
        CNT_PADDING_PG :ASSERT
end:
       0 => A,B,C,D,E,CTX, SP, PC, GAS, MAXMEM, SR, HASHPOS

finalWait:
        ${beforeLast()}  : JMPN(finalWait)

                         : JMP(start)
opINVALID:

3. Polygon zkEVM中的Poseidon哈希函数

设计Poseidon哈希函数（详细见Poseidon哈希函数论文）的目的在于减轻ZKP prover和verifier的计算复杂度。之前定义的KECCAK-256哈希函数由于其不是针对ZKP有限域设计的，需要用大的circuit才能表示。（KECCAK-256在二进制域中运行良好，但在约束设计时将引入大量复杂度。）为此，zkEVM将Poseidon哈希函数作为其内部主要哈希函数。

Polygon zkEVM中使用的Poseidon哈希函数：

• 1）基于的域 F p \mathbb{F}_p Fp​，其中 p = 2 64 − 2 32 + 1 p=2^{64}-2^{32}+1 p=264−232+1。
• 2）Poseidon permutation的state width为8个field elements。（注意，此时改为按完整的field element数，而不是bit数来表示。）对应Polygon zkEVM POSEIDON状态机中为：in0, in1, … , in7。
• 3）相应的capacity为4个field element。对应Polygon zkEVM POSEIDON状态机中为：hashType, cap1, cap2 and cap3。
• 4）Poseidon S-box层使用7-power S-Box，即： S B ( x ) = x 7 , SB(x) = x^7, SB(x)=x7,
• 5）同时，需指定permutation的full round数和partial round数为： R F = 8  (number of full rounds)  , R P = 22  (number of partial rounds) R_F = 8 \text{ (number of full rounds) }, \quad R_P = 22 \text{ (number of partial rounds)} RF​=8 (number of full rounds) ,RP​=22 (number of partial rounds)
• 6）实际实现仅需要一次squeezing迭代，state的前4个field element作为ouput（近似为256-bits，但不会超过256-bits）。
• 7）而Round Constants和MDS matrix可由以上参数完全确定。

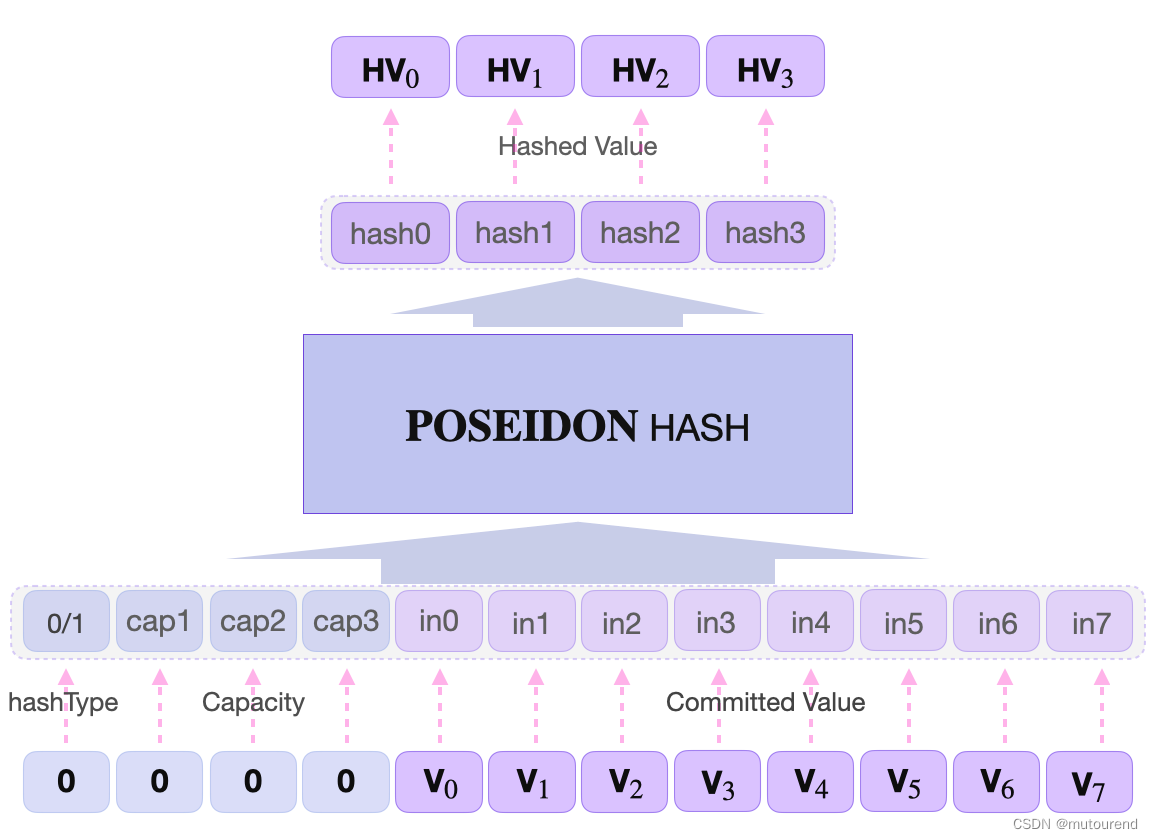
POSEIDON π ^{\pi} π有12个internal state，执行30 rounds，共3次，即总共执行90 rounds。输出为4个哈希值：hash0，hash1，hash2，hash3。 参看Polygon zkEVM zkProver基本设计原则 以及 Storage状态机可知，POSEIDON状态机接收来自 主状态机 和 Storage状态机 中的指令，其需要实现2种哈希函数 H leaf 和 H noleaf H_{\text{leaf}}和H_{\text{noleaf}} Hleaf​和Hnoleaf​，根据hashType为boolean值，其为1，表示选择HASH1作为leaf node哈希函数值；为0，表示选择HASH0作为branch node哈希函数值。

由于POSEIDON哈希输出结果为 4 ∗ ⌊ ( 63.99 ) ⌋  bits = 252 4 * \lfloor(63.99)\rfloor \text{ bits} = 252 4∗⌊(63.99)⌋ bits=252 bits，且有1个bit用于encode each direction，因此，SMT树的level数最大为252。

3.1 Poseidon zkASM示例

以zkevm-proverjs中的poseidon.zkasm为例：【HASHPDIGEST操作符会影响cntPaddingPG和cntPoseidonG计数器；但SLOAD和SSTORE操作符仅影响cntPoseidonG计数器。计数单位均为incCounter。】

start:

        STEP => A
        0 :ASSERT

        ; to verify that there are no correlations between counters
        0 => A
        CNT_ARITH :ASSERT
        CNT_BINARY :ASSERT
        CNT_MEM_ALIGN :ASSERT
        CNT_KECCAK_F :ASSERT
        CNT_POSEIDON_G :ASSERT
        CNT_PADDING_PG :ASSERT

        ; TEST 55 bytes => counter increase 1 => total = 1
		; incCounter=Math.ceil((len+1) / 56)，向上取整。total=0
		; HASHPDIGEST操作符会同时影响cntPaddingPG和cntPoseidonG计数器，计数单位为incCounter
        0 => E
        0 => HASHPOS ; 将位置重置为0
        32 => D ;设置每个HASHP结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E) ; len=len+D=32

        23 => D ;设置每个HASHP结果为23 byte
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511n :HASHP(E) ; len=len+D=32+23=55

        55             :HASHPLEN(E)
        $ => A         :HASHPDIGEST(E)

        1 => A ; incCounter=Math.ceil((55+1)/56)=1。total=total+incCounter=1
        CNT_POSEIDON_G :ASSERT ;  计数单位为incCounter，实际即为total值。
        CNT_PADDING_PG   :ASSERT ;  计数单位为incCounter，实际即为total值。

        ; TEST 56 bytes => counter increase 2 => total = 3

        E + 1 => E
        0 => HASHPOS ; 将位置重置为0
        32 => D ;设置每个HASHP结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E) ; len=len+D=32

        24 => D ;设置每个HASHP结果为24 byte
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9n :HASHP(E) ; len=len+D=32+24=56

        56             :HASHPLEN(E)
        $ => A         :HASHPDIGEST(E)

        3 => A ; incCounter=Math.ceil((56+1)/56)=2。total=total+incCounter=3
        CNT_POSEIDON_G   :ASSERT ;  计数单位为incCounter，实际即为total值。
        CNT_PADDING_PG   :ASSERT ;  计数单位为incCounter，实际即为total值。

        ; TEST 57 bytes => counter increase 2 => total = 5

        E + 1 => E
        0 => HASHPOS ; 将位置重置为0
        32 => D ;设置每个HASHP结果为32 byte

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E) ; len=len+D=32

        25 => D ;设置每个HASHP结果为25 byte
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAn :HASHP(E) ; len=len+D=32+25=57

        57             :HASHPLEN(E)
        $ => A         :HASHPDIGEST(E)

        5 => A ; incCounter=Math.ceil((57+1)/56)=2。total=total+incCounter=5
        CNT_POSEIDON_G   :ASSERT ;  计数单位为incCounter，实际即为total值。
        CNT_PADDING_PG   :ASSERT ;  计数单位为incCounter，实际即为total值。

        ; 0x72913A40CC0E013B4F05C9E8E7A52562CB0FA774C1D1800BDFD5590F83DE53D8n => SR

        0 => SR

        0x23 => A
        0 => B,C
        $ => A  :SLOAD
        0       :ASSERT

        7 => A
        CNT_POSEIDON_G   :ASSERT
        5 => A
        CNT_PADDING_PG   :ASSERT

        0x13 => A
        0x2025 => D
        $ => SR :SSTORE

        11 => A
        CNT_POSEIDON_G   :ASSERT
        5 => A
        CNT_PADDING_PG   :ASSERT

        0x13 => A
        0 => B,C
        $ => A  :SLOAD
        0x2025  :ASSERT

        15 => A
        CNT_POSEIDON_G   :ASSERT
        5 => A
        CNT_PADDING_PG   :ASSERT

        0x23 => A
        ; 0x8026000000000000000000000000000000000000000000000000000000000000n => D
        0x8026n => D
        $ => SR :SSTORE

        25 => A
        CNT_POSEIDON_G   :ASSERT
        5 => A
        CNT_PADDING_PG   :ASSERT

        0x13 => A
        0 => B,C
        $ => A  :SLOAD
        0x2025  :ASSERT

        32 => A
        CNT_POSEIDON_G   :ASSERT
        5 => A
        CNT_PADDING_PG   :ASSERT

        0x23 => A
        0 => B,C
        $ => A  :SLOAD
        ; 0x8026000000000000000000000000000000000000000000000000000000000000n :ASSERT
        0x8026n :ASSERT

        39 => A
        CNT_POSEIDON_G   :ASSERT
        5 => A
        CNT_PADDING_PG   :ASSERT

        ; TEST 111 bytes => counter increase 2 => total = 41/7

        E + 1 => E
        0 => HASHPOS
        32 => D

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        ; 96

        15 => D
        0x5E1268E5B2A8DC1D0BB047386FC227n :HASHP(E)

        111            :HASHPLEN(E)
        $ => A         :HASHPDIGEST(E)

        41 => A
        CNT_POSEIDON_G :ASSERT
        7 => A
        CNT_PADDING_PG   :ASSERT


        ; TEST 112 bytes => counter increase 3 => total = 44/10

        E + 1 => E
        0 => HASHPOS
        32 => D

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        ; 96

        16 => D
        0x5E1268E5B2A8DC1D0BB047386FC227FAn :HASHP(E)

        112            :HASHPLEN(E)
        $ => A         :HASHPDIGEST(E)

        44 => A
        CNT_POSEIDON_G :ASSERT
        10 => A
        CNT_PADDING_PG   :ASSERT

        ; TEST 112 bytes => counter increase 3 => total = 47/13

        E + 1 => E
        0 => HASHPOS
        32 => D

        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        0x5E1268E5B2A8DC1D0BB047386FC227FA4C852DBA596511B9EAF7FCDD79C9006Dn :HASHP(E)
        ; 96

        17 => D
        0x5E1268E5B2A8DC1D0BB047386FC227FA4Cn :HASHP(E)

        113            :HASHPLEN(E)
        $ => A         :HASHPDIGEST(E)

        47 => A
        CNT_POSEIDON_G :ASSERT
        13 => A
        CNT_PADDING_PG   :ASSERT

        ; to verify that there are no correlations between counters

        0 => A
        CNT_ARITH :ASSERT
        CNT_BINARY :ASSERT
        CNT_MEM_ALIGN :ASSERT
        CNT_KECCAK_F :ASSERT

end:
       0 => A,B,C,D,E,CTX, SP, PC, GAS, MAXMEM, SR, HASHPOS

finalWait:
        ${beforeLast()}  : JMPN(finalWait)

                         : JMP(start)
opINVALID:

参考资料

[1] Hashing State Machine [2] The POSEIDON HASH

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom