STARK Low Degree Testing——FRI

1. 引言

前序博客有：

• ZKP大爆炸
• STARKs and STARK VM: Proofs of Computational Integrity
• STARK入门知识
• STARK中的FRI代码解析
• Rescue-Prime hash STARK 代码解析
• Fast Reed-Solomon Interactive Oracle Proofs of Proximity学习笔记

Low Degree Testing低度测试为STARK证明succinctness的秘方。

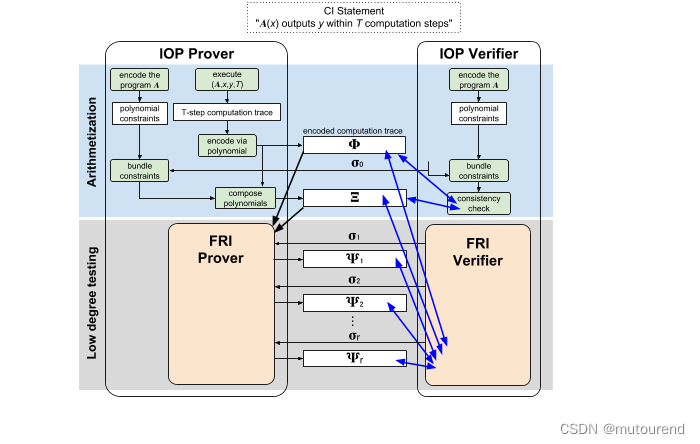在STARK中，通过Arithmetization将Computational Integrity问题reduce为low degree testing问题。

所谓low degree testing低度测试，是指，若要判定某函数是否为具有某指定上限degree的多项式，仅需要make a small number of queries to the function。 低度测试问题已研究了二十多年，是probabilistic proof理论的核心工具。本文重点在于详细解释低度测试，并介绍FRI协议——STARK中所用的低度测试解决方案。

2. 低度测试

低度测试针对的场景为： 给定某函数，仅查询该函数的 “少量” 位置，来判定该函数是否为 小于某常量 d d d degree的某多项式。

即，已知某域 F F F的子集 L L L和degree bound d d d，判定 f : L → F f:L\rightarrow F f:L→F是否等于某degree小于 d d d的多项式，即，是否存在多项式： p ( x ) = c 0 + c 1 x + ⋯ + c d − 1 x d − 1 p(x)=c_0+c_1x+\cdots+c_{d-1}x^{d-1} p(x)=c0​+c1​x+⋯+cd−1​xd−1 over F F F，其中对于 ∀ a ∈ L \forall a\in L ∀a∈L，有 p ( a ) = f ( a ) p(a)=f(a) p(a)=f(a)。 可想象field size很大，如为 2 128 2^{128} 2128， L L L的size约为1千万（10,000,000）。

为解决该问题，需要query f f f at 整个 L L L域，因 f f f可能仅在 L L L中的某个单点不满足 p ( a ) = f ( a ) p(a)=f(a) p(a)=f(a)。即使我们允许一定概率的错误，所需query的次数仍然与 L L L的size呈线性关系。

低度测试，通过构建probabilistic proof，将query number降为logarithmic in ∣ L ∣ |L| ∣L∣（如 L ≈ 10 , 000 , 000 ，则 log ⁡ 2 ( L ) ≈ 23 L\approx10,000,000，则\log_2(L)\approx 23 L≈10,000,000，则log2​(L)≈23），可解决上述问题。确切来说，分为如下2种情况：

• 1）第一种情况——若函数 f f f等于某低度多项式：即存在多项式 p ( x ) p(x) p(x) over F F F，其degree小于 d d d，并agrees with f f f everywhere on L L L。
• 2）第二种情况——若函数 f f f为far from ALL low degree polynomials：如，需调整 f f f中至少 10 % 10\% 10%的值，才能获得一个与degree小于 d d d多项式一致的函数 f ′ f' f′。

还有一种可能性是：

• 3）第三种情况——若函数 f f f中度接近某低度多项式，但不等于任何低度多项式。如，某函数具有 5 % 5\% 5%的值不等于低度多项式，因此不符合以上两种情况。但是，之前的STARK arithmetization步骤中，确保了本情况不会发生。即，诚实的Prover在处理true statement算术化过程中，会落入第一种情况；而作弊的Prover在试图证明false claim时，将大概率落入第二种情况。

为了区分以上两种情况，将使用a probabilistic polynomial-time test来query f f f at a small number of locations。

【

• 若 f f f确实是低度的，则该测试通过的概率为 1 1 1。
• 若 f f f为far from low degree，则该测试将大概率不通过。
• 若 f f f为 δ \delta δ-far from any function degree less than d d d（即，必须修改至少 δ ∣ L ∣ \delta|L| δ∣L∣ 个位置来获得某个degree小于 d d d的多项式），则测试被拒绝的概率不低于 Ω ( δ ) \Omega({\delta}) Ω(δ)（或其它“nice” function of δ \delta δ）。直观来说，若 δ \delta δ越接近零，则区分这两种情况的难度越大。 】

接下来将一种简单的低度测试方案，并解释其为何无法满足要求，然后介绍一种效率指数级提升的复杂低度测试方案——STARK中使用的FRI。

2.1 Direct Test 低度测试方案

Direct Test 低度测试方案是： 通过采用 d + 1 d+1 d+1次query，来判断某函数是否为（或接近为）某degree小于 d d d的多项式。

Direct Test 低度测试方案 基于的多项式basic fact为：

• 任意degree小于 d d d的多项式，可由 F F F中任意 d d d个不同位置的值唯一确定。

该fact源自：degree为 k k k的多项式，最多具有 k k k个roots in F F F。

Direct Test 低度测试方案中，query次数为 d + 1 d+1 d+1，远小于 f f f的domain size ∣ L ∣ |L| ∣L∣。

首先讨论2个简单的特例情况：

• 1）若函数 f f f为constant function，即 d = 1 d=1 d=1：则低度测试问题转为区分 f f f为某constant function（ f ( x ) = c f(x)=c f(x)=c for some c c c in F F F） 还是 f f f为far from any constant function。 针对这种特例情况，仅需要2-query test即可：query f f f at 某固定点 z 1 z_1 z1​以及某随机点 w w w，然后检查 f ( z 1 ) = f ( w ) f(z_1)=f(w) f(z1​)=f(w)是否成立即可。直观的， f ( z 1 ) f(z_1) f(z1​)可决定 f f f的常量值， f ( w ) f(w) f(w)测试是否所有的 f f f都接近该常量值。

• 2）若函数 f f f为线性函数，即 d = 2 d=2 d=2：则低度测试问题转为区分 f f f为某线性函数（ f ( x ) = a x + b f(x)=ax+b f(x)=ax+b for some a , b a,b a,b in F F F） 还是 f f f为far from any linear function。 针对这种特例情况，仅需要3-query test即可：query f f f at 某2个固定点 z 1 , z 2 z_1,z_2 z1​,z2​以及某随机点 w w w，然后检查 ( z 1 , f ( z 1 ) ) , ( z 2 , f ( z 2 ) ) , ( w , f ( w ) ) (z_1,f(z_1)),(z_2,f(z_2)),(w,f(w)) (z1​,f(z1​)),(z2​,f(z2​)),(w,f(w))是否共线性。直观的， f ( z 1 ) 和 f ( z 2 ) f(z_1)和f(z_2) f(z1​)和f(z2​)可决定 f f f线性函数， f ( w ) f(w) f(w)测试所有 f f f值是否都在该线上。

将以上特例情况推广至具有degree bound d d d的通用情况： query f f f at d d d个固定点 z 1 , z 2 , ⋯   , z d z_1,z_2,\cdots,z_d z1​,z2​,⋯,zd​以及某随机点 w w w。根据 f f f在 z 1 , z 2 , ⋯   , z d z_1,z_2,\cdots,z_d z1​,z2​,⋯,zd​的 d d d个值，可唯一确定degree小于 d d d的多项式 h ( x ) h(x) h(x) over F F F that agrees with f f f at these points。然后检查随机点的 h ( w ) = f ( w ) h(w)=f(w) h(w)=f(w)是否成立即可，因此称为Direct Test。

根据定义可知，若 f ( x ) f(x) f(x)等于 某degree小于 d d d的多项式 p ( x ) p(x) p(x)，则 h ( x ) h(x) h(x)等于 p ( x ) p(x) p(x)，Direct Test被通过的概率为 1 1 1。该属性称为“完美完备性”，即意味着Direct Test具有only 1-sided error。

接下来讨论，若 f f f为 δ \delta δ-far from any function of degree less than d d d的情况，如假设 δ = 10 % \delta=10\% δ=10%。此时，Direct Test被拒绝的概率不低于 δ \delta δ。通过随机选择 w w w，使得 h ( w ) ≠ f ( w ) h(w)\neq f(w) h(w)=f(w)的概率为 μ \mu μ，则 μ \mu μ必须不小于 δ \delta δ。

【反向证明，若 μ \mu μ小于 δ \delta δ，则可推论 f f f为 δ \delta δ-close to h h h，与 f f f为 δ \delta δ-far from any function of degree less than d d d的前提情况矛盾。】

2.2 Direct Test低度测试方案不足以满足需求

因STARK中的testing函数 f : L → F f:L\rightarrow F f:L→F中编码了computation traces，其degree d d d（和domain L L L）非常大，若直接运行query d + 1 d+1 d+1次的Direct Test，将是非常昂贵的。 为此，为指数级（相对于computation trace size）的节约STARK中Verifier的验证时间，需要将 d + 1 d+1 d+1次 reduce为仅需 O ( log ⁡ d ) O(\log d) O(logd)次query。

但是，若query f f f at 小于 d + 1 d+1 d+1个位置，将无法得出任何结论。

【 方案之一是，考虑函数 f : L → F f:L\rightarrow F f:L→F的2种不同分布：

• 分布一：uniformly选择一个degree正好为 d d d的多项式，并对其evaluate on L L L。
• 分布二：对于任意 d d d个点 z 1 , z 2 , ⋯   , z d z_1,z_2,\cdots,z_d z1​,z2​,⋯,zd​，其值 f ( z 1 ) , f ( z 2 ) , ⋯   , f ( z d ) f(z_1),f(z_2),\cdots,f(z_d) f(z1​),f(z2​),⋯,f(zd​)为均匀独立分布的。

即意味着从信息轮角度来将，即使借助某test也无法区分以上2种分布（since polynomials from the first distribution should be accepted by the test while those of degree exactly d are very far from all polynomials of degree less than d, and thus should be rejected）。 】

2.3 引入Prover

已知，若要测试某函数 f : L → F f:L\rightarrow F f:L→F close to某degree小于 d d d的多项式，需要 d + 1 d+1 d+1次query，但是我们无法承担那么多的query次数。

将该低度测试问题转换为： 某Prover可提供关于函数 f f f的有用辅助信息。

通过引入Prover，可将低度测试的query次数实现指数级改进，所需query次数降为 O ( log ⁡ d ) O(\log d) O(logd)。

具体协议为：

• （untrusted）Prover：直到待测试的整个函数 f f f。
• Verifier：查询函数 f f f的少量位置，并希望借助Prover的帮助，但不需要信任Prover是诚实的。即意味着Prover可能会作弊且不遵循该协议，但Prover一旦作弊，Verifier有权拒绝，无论函数 f f f是否为低度的。关键点在于，除非 f f f确实是低度的，否则Verifier不会被说服。

可将上面的Direct Test看成是Prover啥也没干的特例情况，Verifier没有任何人辅助，自行测试该函数是否为低度多项式。为此，需充分有效利用Prover的功能，使得效率比Direct Test要高。

在整个协议中，Prover将want to enable the Verifier to query auxiliary functions on locations of the Verifier’s choice。可通过“commitment”来达成。即，Prover可将其选择的函数commit为a Merkle tree，然后Verifier可要求Prover公开该committed函数的任意位置集。这种承诺机制的主要属性在于：一旦Prover对某函数commit之后，其必须公开正确的值，且无法作弊（即，其无法在看到Verifier发来的请求位置之后再决定函数的值）。

2.4 2个函数的情况下将query次数减半

接下来将举例说明在Prover的帮助下如何将query次数减半。

假设有2个多项式 f , g f,g f,g，想要证明 f 和 g f和g f和g的degree都小于 d d d，若运行Direct Test，则需要分别对 f , g f,g f,g进行query，一共需要 2 ∗ ( d + 1 ) 2*(d+1) 2∗(d+1)次query。接下来将说明如何将query次数降为 ( d + 1 ) (d+1) (d+1)再加某smaller-order term。

• 1）Verifier选择随机值 α \alpha α发送给Prover；
• 2）Prover将 h ( x ) = f ( x ) + α g ( x ) h(x)=f(x)+\alpha g(x) h(x)=f(x)+αg(x)在domain L L L进行evaluate，并将evaluation值进行commit后发送给Verifier（实时上，Prover将 ∀ x ∈ L \forall x\in L ∀x∈L的所有 h ( x ) h(x) h(x)值作为叶子节点构建Merkle tree，将相应Merkle tree root发送给了Verifier）；【注意此处的domain L L L仍为函数 f f f的domain L L L】
• 3）Verifier现在可通过Direct Test测试 h h h的degree是否小于 d d d，需要的查询次数为 d + 1 d+1 d+1。

直观的，若 f f f或 g g g的degree不小于 d d d，则大概率 h h h的degree也不小于 d d d。 如，假设 f f f的 x n x^n xn项系数不为零，且 n ≥ d n\geq d n≥d，则最多仅有一个 α \alpha α取值（由Verifier选择发送），使得 h h h的 x n x^n xn项系数为零，即意味着 h h h degree小于 d d d的概率约为 1 / ∣ F ∣ 1/|F| 1/∣F∣。若field足够大，如 ∣ F ∣ > 2 128 |F|>2^{128} ∣F∣>2128，该错误概率可忽略。

不过，我们在第3）步中，并不检查 h h h为某degree小于 d d d的多项式，而转为仅检查 h h h close to 某degree小于 d d d的多项式。这就意味着以上分析并不准确。是否有可能 f f f为far from a low degree polynomial and the linear combination h h h will be close to one with a non-negligible probability over α \alpha α？答案是不可能，详细可阅读 2017年论文Ligero: Lightweight Sublinear Arguments Without a Trusted Setup 以及 2018年论文Fast Reed-Solomon Interactive Oracle Proofs of Proximity。

此外，Verifier如何知道Prover发来的多项式 h h h的形式为 f ( x ) + α g ( x ) f(x)+\alpha g(x) f(x)+αg(x)？恶意Prover可发送确实是低度的多项式，但是不同于Verifier请求的多项式线性组合 f ( x ) + α g ( x ) f(x)+\alpha g(x) f(x)+αg(x)。若已知 h h h close to 某低度多项式，然后测试该低度多项式具有正确的形式：

• Verifier：随机选择 L L L中的点 z z z，然后query f , g , h f,g,h f,g,h at z z z，然后检查 h ( z ) = f ( z ) + α g ( z ) h(z)=f(z)+\alpha g(z) h(z)=f(z)+αg(z)成立即可。这个测试应该重复多次，以提高测试的准确性，但误差随着样本数量的增加而呈指数级缩小。因此，这一步骤仅将查询数量（到目前为止是d+1），增加了一个smaller-order term。

2.5 将单个多项式切分为2个smaller-degree多项式

根据2.4可知，借助Prover的帮助，可将测试2个多项式degree均小于 d d d的query次数，由 2 ∗ ( d + 1 ) 2*(d+1) 2∗(d+1) 降为 d + 1 d+1 d+1。 接下来，描述，如何将degree小于 d d d的多项式 切分为 2个degree小于 d / 2 d/2 d/2的多项式。

令 f ( x ) f(x) f(x)为degree小于 d d d的多项式，且 d d d为偶数。 则有 f ( x ) = g ( x 2 ) + x h ( x 2 ) f(x)=g(x^2)+xh(x^2) f(x)=g(x2)+xh(x2)，其中 g ( x ) , h ( x ) g(x),h(x) g(x),h(x)的degree均小于 d / 2 d/2 d/2。事实上，可令 g ( x ) g(x) g(x)由 f ( x ) f(x) f(x)的偶数项系数组成， h ( x ) h(x) h(x)由 f ( x ) f(x) f(x)的奇数项系数组成。

如，令 d = 6 d=6 d=6，有： f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5 f(x)=a0​+a1​x+a2​x2+a3​x3+a4​x4+a5​x5 有： g ( x ) = a 0 + a 2 x + a 4 x 2 g(x)=a_0+a_2x+a_4x^2 g(x)=a0​+a2​x+a4​x2 h ( x ) = a 1 + a 3 x + a 5 x 2 h(x)=a_1+a_3x+a_5x^2 h(x)=a1​+a3​x+a5​x2 为 n ∗ log ⁡ ( n ) n*\log(n) n∗log(n) algorithm for polynomial evaluation（若直接计算，为 n 2 n^2 n2 algorithm）。

2.6 FRI协议

以上已形成了2种思想：

• 1）以一半的query次数，实现对2个多项式的低度测试；
• 2）将单个多项式切分为2个度数更低的多项式。

FRI协议（全称为Fast Reed-Solomon Interactive Oracle Proofs of Proximity，详细可参看2018年论文Fast Reed-Solomon Interactive Oracle Proofs of Proximity）为将这2种思想结合，仅需要 O ( log ⁡ d ) O(\log d) O(logd)次query，可测试某函数 f f f具有（准确来说是close to）degree小于 d d d。

为简单起见，令 d d d为a power of 2 2 2。 FRI协议包含2个阶段：

• 1）Commit阶段
• 2）Query阶段

2.6.1 FRI协议的Commit阶段

FRI协议的Commit阶段为：

• 1）Prover将原始的 f 0 = f ( x ) f_0=f(x) f0​=f(x)多项式切分为2个degree小于 d / 2 d/2 d/2的多项式 g 0 ( x ) , h 0 ( x ) g_0(x),h_0(x) g0​(x),h0​(x)，使得 f 0 ( x ) = g 0 ( x 2 ) + x h 0 ( x 2 ) f_0(x)=g_0(x^2)+xh_0(x^2) f0​(x)=g0​(x2)+xh0​(x2)。
• 2）Verifier发送随机值 α 0 \alpha_0 α0​。
• 3）Prover对多项式 f 1 ( x ) = g 0 ( x ) + α 0 h 0 ( x ) f_1(x)=g_0(x)+\alpha_0 h_0(x) f1​(x)=g0​(x)+α0​h0​(x)进行commit。注意此时 f 1 ( x ) f_1(x) f1​(x)的degree小于 d / 2 d/2 d/2。【 f 1 ( x ) f_1(x) f1​(x)的evaluation值是不是基于 L L L，而是基于 L 2 = { x 2 : x ∈ L } L^2=\{x^2:x\in L\} L2={x2:x∈L}。】
• 4）Prover将原始的 f 1 f_1 f1​多项式切分为2个degree小于 d / 2 d/2 d/2的多项式 g 1 ( x ) , h 1 ( x ) g_1(x),h_1(x) g1​(x),h1​(x)，使得 f 1 ( x ) = g 1 ( x 2 ) + x h 1 ( x 2 ) f_1(x)=g_1(x^2)+xh_1(x^2) f1​(x)=g1​(x2)+xh1​(x2)。
• 5）Verifier发送随机值 α 1 \alpha_1 α1​。
• 6）Prover对多项式 f 2 ( x ) = g 1 ( x ) + α 1 h 1 ( x ) f_2(x)=g_1(x)+\alpha_1 h_1(x) f2​(x)=g1​(x)+α1​h1​(x)进行commit。注意此时 f 2 ( x ) f_2(x) f2​(x)的degree小于 d / 4 d/4 d/4。
• 7）……

重复以上过程，每一次切分，多项式degree都会减半。使得 log ⁡ ( d ) \log (d) log(d)步之后，可获得一个constant多项式，Prover仅需将该常量值发送给Verifier。

不过，要注意domain：

• 1）以上协议中，要求 ∀ z ∈ L \forall z\in L ∀z∈L，有 − z ∈ L -z\in L −z∈L。
• 2） f 1 ( x ) f_1(x) f1​(x)的evaluation值是不是基于 L L L，而是基于 L 2 = { x 2 : x ∈ L } L^2=\{x^2:x\in L\} L2={x2:x∈L}。然后基于这些evaluation值构建Merkle tree commitment。
• 3）递归调用以上FRI step， L 2 L^2 L2需满足 { z , − z } \{z,-z\} {z,−z}属性。

这些要求很容易选择domain L L L来满足（即，某size为a power of 2 2 2的multiplicative subgroup即可满足），而事实上，巧合的是，与高效FFT算法的要求一致（STARK中对execution trace进行编码时，有用到FFT算法）。

2.6.2 FRI协议的Query阶段

FRI协议的Query阶段，是为了检查Prover没有作弊。 Verifier选择 L L L中的随机点 z z z，query f 0 ( z ) 和 f 0 ( − z ) f_0(z)和f_0(-z) f0​(z)和f0​(−z)。这2个值足以确定 g 0 ( z 2 ) 和 h 0 ( z 2 ) g_0(z^2)和h_0(z^2) g0​(z2)和h0​(z2)的值，因可将其看成是2个线性方程式，以“ g 0 ( z 2 ) 和 h 0 ( z 2 ) g_0(z^2)和h_0(z^2) g0​(z2)和h0​(z2)”为变量： f 0 ( z ) = g 0 ( z 2 ) + z h 0 ( z 2 ) f_0(z)=g_0(z^2)+zh_0(z^2) f0​(z)=g0​(z2)+zh0​(z2) f 0 ( − z ) = g 0 ( z 2 ) − z h 0 ( z 2 ) f_0(-z)=g_0(z^2)-zh_0(z^2) f0​(−z)=g0​(z2)−zh0​(z2)

Verifier可解这2个方程式，然后推断出 g 0 ( z 2 ) 和 h 0 ( z 2 ) g_0(z^2)和h_0(z^2) g0​(z2)和h0​(z2)的值。同时，因 f 1 ( x ) = g 0 ( x ) + α 0 h 0 ( x ) f_1(x)=g_0(x)+\alpha_0 h_0(x) f1​(x)=g0​(x)+α0​h0​(x)，有 f 1 ( z 2 ) = g 0 ( z 2 ) + α 0 h 0 ( z 2 ) f_1(z^2)=g_0(z^2)+\alpha_0 h_0(z^2) f1​(z2)=g0​(z2)+α0​h0​(z2)，从而可知 f 1 ( z 2 ) f_1(z^2) f1​(z2)也为 g 0 ( z 2 ) 和 h 0 ( z 2 ) g_0(z^2)和h_0(z^2) g0​(z2)和h0​(z2)的线性组合。此时，Verifier可query f 1 ( z 2 ) f_1(z^2) f1​(z2)，并自行基于 g 0 ( z 2 ) 和 h 0 ( z 2 ) g_0(z^2)和h_0(z^2) g0​(z2)和h0​(z2)的线性组合计算，判断二者是否相等。从而确定Prover在commit阶段发送的 f 1 ( x ) f_1(x) f1​(x)的承诺值确实是正确的。 Verifier可继续，进一步query f 1 ( − z 2 ) f_1(-z^2) f1​(−z2)（注意， − z 2 ∈ L 2 -z^2\in L^2 −z2∈L2且 f 1 ( x ) f_1(x) f1​(x)的commitment是基于 L 2 L^2 L2的），从而推导出 f 2 ( z 4 ) f_2(z^4) f2​(z4)。

Verifier可重复以上过程，直到最终推导出 f log ⁡ d ( z ) f_{\log d}(z) flogd​(z)的值，其为constant 多项式，其constant值由Prover在commit阶段发送（在Verifier发送 z z z之前）。Verifier需检查其收到的值 与 其根据之前query到的函数计算出来的值 是确实相等的。

总之，总的query次数为 log ⁡ d \log d logd。

【 为何Prover无法作弊呢？ 假设 f 0 f_0 f0​ is zero on 90 % 90\% 90% of the pairs of the form { z , − z } \{z,-z\} {z,−z}，即 f 0 ( z ) = f 0 ( − z ) = 0 f_0(z)=f_0(-z)=0 f0​(z)=f0​(−z)=0（称这种为“good” pairs）。而仍有 10 % 10\% 10%的为非零值（称为“bad” pairs）。 Verifier在随机选择query z z z时，有 10 % 10\% 10%的概率落入bad pair，但是，仅有一个 α \alpha α取值能使得 f 1 ( z 2 ) = 0 f_1(z^2)=0 f1​(z2)=0，其余的 α \alpha α取值都将导致 f 1 ( z 2 ) ≠ 0 f_1(z^2)\neq 0 f1​(z2)=0。若Prover在 f 1 ( z 2 ) f_1(z^2) f1​(z2)上作弊，将被抓获。因此， ( f 1 ( z 2 ) , f 1 ( − z 2 ) ) (f_1(z^2),f_1(-z^2)) (f1​(z2),f1​(−z2))在下一层中也将大概率为bad pair（当 f 1 ( z 2 ) ≠ 0 f_1(z^2)\neq 0 f1​(z2)=0时， f 1 ( − z 2 ) ) f_1(-z^2)) f1​(−z2))的值已不重要了）。如此持续，最后一层中的值为非零值的概率将很高。 】

不过，另一方面，若某函数具有 90 % 90\% 90%的零值，则Prover将无法get close to a low degree polynomial other than the zero polynomial（该fact此处不证明）。特别的，这意味着在最后一层Prover必须发送0值。但是，Verifier仅有约 10 % 10\% 10%的概率来抓获Prover作弊。这仅是一个非正式论证，详细证明可参看2018年论文Fast Reed-Solomon Interactive Oracle Proofs of Proximity。

目前为止，以上测试Verifier抓获恶意Prover的概率仅为10%，即错误概率为 90 % 90\% 90%，但是，对多个独立sample的 z z z值，重复以上query阶段，可指数级提升准确率。如，选择850个query z z z值，错误概率可降为 2 − 128 2^{-128} 2−128，可几乎忽略不计。

3. 总结

本文主要描述了低度测试问题。 若采用Direct Test低度测试方案，所需的query次数过多，无法满足STARK所需的succinct要求。 为实现logarithmic query complexity，采用了名为FRI的交互协议，引入Prover添加信息，使得Verifier可信服该函数确实是低度的。

事实上，FRI使得Verifier可以 log ⁡ d \log d logd次query，来解决低度测试问题。

参考资料

[1] StarkWare 2019年博客 Low Degree Testing [2] StarkWare 2019年博客 A Framework for Efficient STARKs