STARK Arithmetization

1. 引言

前序博客有：

• ZKP大爆炸
• STARKs and STARK VM: Proofs of Computational Integrity
• STARK入门知识
• STARK中的FRI代码解析
• Rescue-Prime hash STARK 代码解析
• Fast Reed-Solomon Interactive Oracle Proofs of Proximity学习笔记
• STARK Low Degree Testing——FRI

通过本文，将理解如何将Computational Integrity statement转换为：

• 1）execution trace；
• 2）polynomia constraints多项式约束。

2. 初识STARK

STARK协议的目标是：

• verify computations succinctly and transparently。

STARK的第一步称为Arithmetization：

• 用于将待验证的计算问题 转换为 检查特定的低度多项式问题，使得Verifier端可高效验证（即“succinctly”验证）。

算术化是有用的，因为它可以使用纠错码领域的工具，有效地进行低度测试。 但是算术化本身近似将Computational Integrity statement转换为某多项式，然后Prover需要通过STARK Low Degree Testing——FRI 交互协议来使Verifier信服该多项式确实是低度的。当且仅当原始计算是正确时（除外概率很低），Verifier才信服该多项式是低度的。STARK最后一步会将FRI交互协议转换为非交互协议，可将相应的非交互STARK提交到链上并由任何人公开验证。

Arithmetization算术化本身分为2个阶段：

• 1）生成execution trace和多项式约束；
• 2）将execution trace和多项式约束合并为一个单一的低度多项式。

Prover和Verifier交互过程中，实际是对多项式约束达成共识。然后Prover生成execution trace，并在后续的交互过程中，Prover试图说服Verifier其execution trace满足该多项式承诺，尽管execution trace对Verifier是不可见的。

2. 回顾Computational Integrity Statements

传统的Computational Integrity Statements举例为：如，给超市的付款总金额计算正确，传统的proof是如下的收据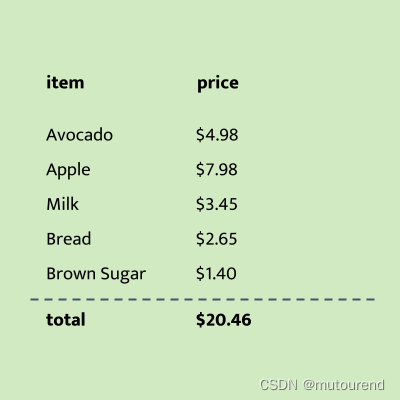： 收据中包含每项内容及相应的价格，总金额列在最下面。

简单起见，将该statement理解为：求和计算正确。 为验证该statement是否成立，方法之一对着收据逐项求和，检查最终的值是否与收据下方的值一致。

3. Arithmetization第一阶段——代数表示

算术化的第一阶段是将某CI statement（如“区块7218290内的第15笔交易是正确的”），转换为 formal algebraic language。

主要有2个目的：

• 1）以非模糊的方式简洁地定义了该claim；
• 2）将该claim嵌入到某algebraic domain。这种嵌入需要借助算术化第二阶段，来将某CI statement reduce为 关于特定degree多项式的claim。

algebraic表示时通常有2大要素：

• 1）an execution trace：为表示每步底层计算的表，其中每行对应一步。
• 2）a set of polynomial constraints：构建了一组多项式约束，使得当且仅当该execution trace表示了有效的计算时，这些约束才满足。

execution trace可能很长，但多项式约束可比较精简。

3.1 Execution Trace

所生成的execution trace应易于精简测试，应具有如下两个特点：

• 1）每行都可仅依赖trace中的相邻行进行验证；
• 2）每组pair of rows可应用相同的验证流程。

以上两个特点将直接影响STARK proof size。 仍然以超市收据为例，来说明何为易于精简测试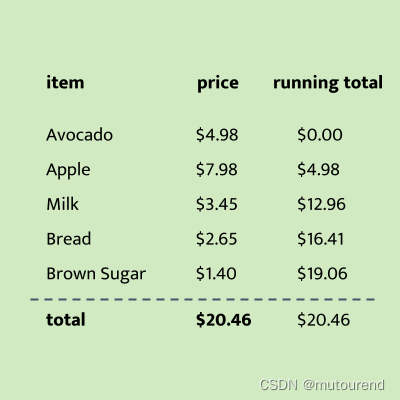： 通过引入新的一列“running total”，使得可在已知previous row的情况下，独立验证每一行。

如在计算中检查这2行： 仅需检查12.96+3.45=16.41即可。注意，对于每组pair of rows，都可使用相同的约束，我们将其称为succinct constraints。

3.2 Polynomial Constraints

将添加了新列的超市收据以table表示为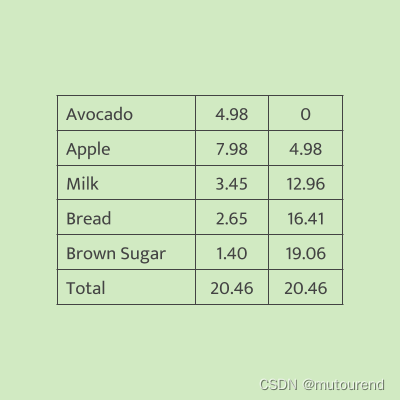： 将第 i i i行第 j j j列的单元格值表示为 A i , j A_{i,j} Ai,j​，从而可将求和正确性 改写为 一组多项式约束：

• 1） A 0 , 2 = 0 A_0,2=0 A0​,2=0，因初始running total值应为0；
• 2） ∀ 1 ≤ i ≤ 5 : A i , 2 − A i − 1 , 2 − A i − 1 , 1 = 0 \forall 1\leq i\leq 5: A_{i,2}-A_{i-1,2}-A_{i-1,1}=0 ∀1≤i≤5:Ai,2​−Ai−1,2​−Ai−1,1​=0，每一行的running total值都计算正确；【为同一约束执行多次】
• 3） A 5 , 1 − A 5 , 2 = 0 A_{5,1}-A_{5,2}=0 A5,1​−A5,2​=0，最后一行的running total值即为总额。

这些即为 A i , j A_{i,j} Ai,j​的线性多项式约束。若所使用的多项式为high degree，则对proof length和生成证明所需时间 都有反向作用。因此，线性约束是我们所希望的最好状态。

多项式约束的size与收据的长度无关。

从而，将验证超市收据总额的CI problem，转换为一个精简易于测试的execution trace，以及相应的一组多项式约束，使得当前仅当原始收据的总额是正确的，这组多项式约束才成立。

3.3 更复杂的举例——Collatz Conjecture

1937年，德国名为Lothar Collatz的数学家在数论领域提出了Collatz Conjecture。初看这是一个可爱的数学谜题，但实际上，它是数论领域的一个公开难题。数年来它吸引了很多数学家的注意，获得了大量同义词（如the 3n + 1 conjecture, the Ulam conjecture, Kakutani’s problem等等）。Paul Erdős曾评论称：“Mathematics may not be ready for such problems”。

Collatz数列以任意正整数开始，其中后续元素的计算规则为：

• 1）若前一元素为偶数，将其除2；
• 2）若前一元素为奇数且大于1，则将其乘以3再加1；
• 3）若前一元素为1，则停止。

以初始值为52为例，有： 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1.

Collatz Conjecture是指：以任意正整数开始，最终Collatz数列都将达到1值。

不过，Collatz Conjecture本身并不在本文考虑范畴，本文重点关注：如何验证以某特定整数开始的Collatz数列计算正确。

3.3.1 Collatz数列 Execution Trace

Collatz数列的CI statement为： “A Collatz sequence that starts with 52, ends with 1 after 11 iterations”。

令 A A A为该数列计算的execution trace，第 i i i行表示为 A i A_i Ai​，对应为该数列中的第 i i i个元素。所有元素都以二进制表示，使得其易于在多项式中表示其奇偶性。以 A i , j A_{i,j} Ai,j​表示数列中第 i i i个元素的第 j j j个最低有效位。如 A 0 = 001011 A_0=001011 A0​=001011表示初始值52（注意52的二进制表示为1101001，在此处以逆序表示，以简化后续多项式约束中的索引）。

对应的execution trace为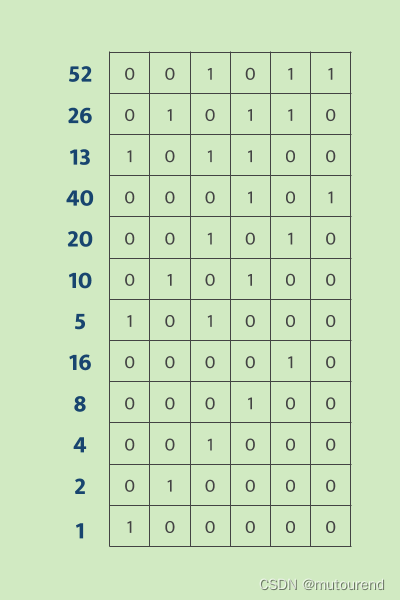： 注意，该trace中仅有6列，是因为6个bit就足以表达该数列中的最大值了。若初始值为51，则最大值为154，相应的trace表示需引入8列。

3.3.2 Collatz数列多项式约束

当且仅当trace A中描述了指定的Collatz数列（以52开始，以1结束，相邻2行的transition计算正确），相应的多项式约束才成立。 本例中，trace A的size为6x12，即表示Collatz数列中有12个6-bit数字，相应的多项式约束为：【 n = 12 , m = 6 n=12,m=6 n=12,m=6】 前三个约束很直观：

• 1）第一个约束第一行初始值的二进制表示为52；
• 2）第二个约束最后一行的二进制表示为1；
• 3）第三个约束trace中所有值均为bits，仅可取0或1值；
• 4）第4个约束是表示该序列succinct computation的核心，即表示了every相邻行之间的关联。将计算约束表示为局部约束的循环模式（即简洁性）的能力是Verifier比计算的简单重放快指数的基础。【The ability to express computational constraints as a recurring pattern of local constraints (i.e. succinctness), is fundamental to the verifier being exponentially faster than a naive replay of the computation.】

接下来仔细检查这些约束，对于任意的 i < n − 1 i