布隆过滤器原理和实现

一、布隆过滤器介绍

巴顿.布隆于一九七零年提出

一个很长的二进制向量 （位数组）

一系列随机函数 (哈希)

空间效率和查询效率高

有一定的误判率（哈希表是精确匹配）

二、布隆过滤器原理

布隆过滤器（Bloom Filter）的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m，哈希函数的个数为k

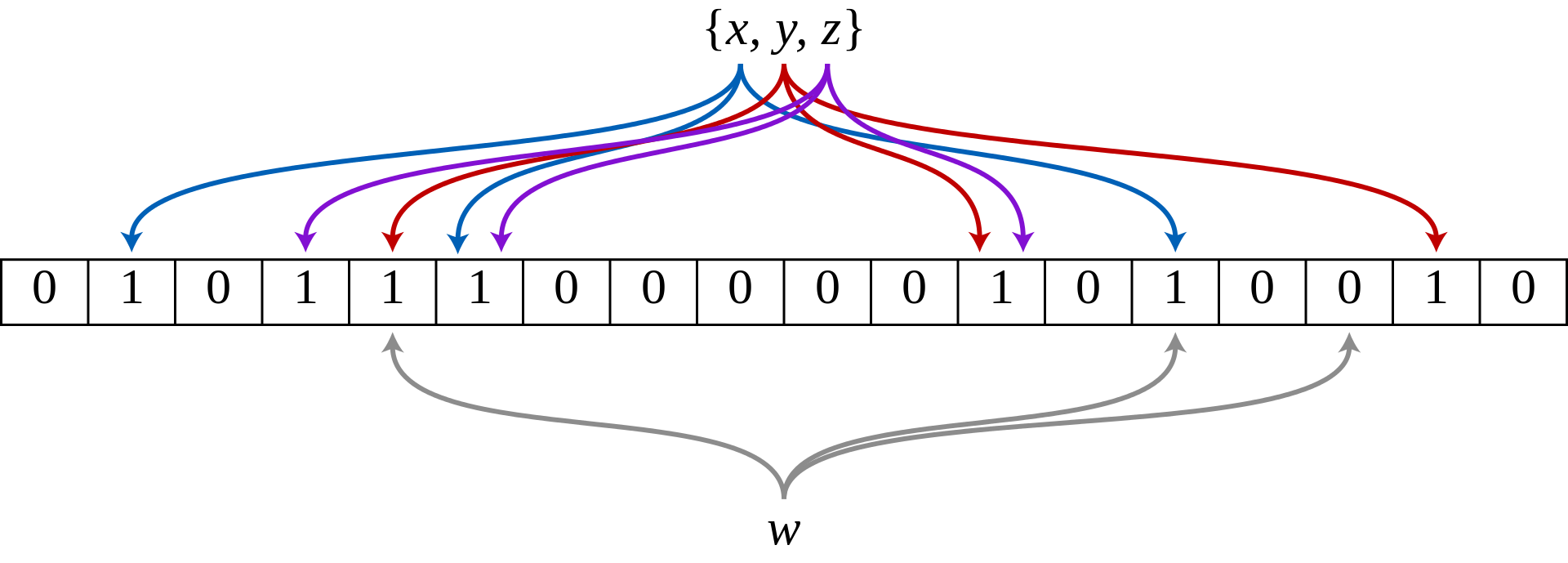
以上图为例，具体的操作流程：

假设集合里面有3个元素{x, y, z}，哈希函数的个数为3。

首先将位数组进行初始化，将里面每个位都设置位0。

对于集合里面的每一个元素，将元素依次通过3个哈希函数进行映射，每次映射都会产生一个哈希值，这个值对应位数组上面的一个点，然后将位数组对应的位置标记为1。

查询W元素是否存在集合中的时候，同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1，则可以判断该元素一定不存在集合中。

反之，如果3个点都为1，则该元素可能存在集合中。

注意：此处不能判断该元素是否一定存在集合中，可能存在一定的误判率。

可以从图中可以看到：

假设某个元素通过映射对应下标为4，5，6这3个点。虽然这3个点都为1，但是很明显这3个点是不同元素经过哈希得到的位置，

因此这种情况说明元素虽然不在集合中，也可能对应的都是1，这是误判率存在的原因。

三、布隆过滤器添加元素

将要添加的元素给k个哈希函数

得到对应于位数组上的k个位置

将这k个位置设为1

四、布隆过滤器查询元素

将要查询的元素给k个哈希函数

得到对应于位数组上的k个位置

如果k个位置有一个为0，则肯定不在集合中

如果k个位置全部为1，则可能在集合中

五、布隆过滤器实现

public class BloomFilter {
    public static final int NUM_SLOTS=1024*1024*8;
    public static final int NUM_HASH=8;
    private BigInteger bitmap = new BigInteger("0");

    public static void main(String[] args) {
        //测试代码
        BloomFilter bf = new BloomFilter();
        ArrayList contents = new ArrayList();
        contents.add("sldkjelsjf");
        contents.add("ggl;ker;gekr");
        contents.add("wieoneomfwe");
        contents.add("sldkjelsvrnlkjf");
        contents.add("ksldkflefwefwefe");

        for(int i=0;i