数据结构大致分为以下几种存储结构：
- 线性表(Linear table) 1.1 顺序表 1.2 链表 1.3 栈/队列
- 树结构(tree structure) 1.1 普通树 1.2 二叉树 1.3 线索二叉树
- 图存储结构(Graph storage structure)
线性表结构存储的数据往往是可以依次排序的，就像小朋友手拉手，每位学生的前面和后面都仅有一个小朋友和他拉手，具备这种 “一对一” 关系的数据就可以使用线性表来存储。 
例如，存储类似 {1,3,5,7,9} 这样的数据时，各元素依次排列，每个元素的前面和后边有且仅有一个元素与之相邻（除首元素和尾元素），因此可以使用线性表存储。
线性表并不是一种具体的存储结构，它包含顺序存储结构和链式存储结构，是顺序表和链表的统称。
顺序表(Sequence table)
顺序表，简单地理解，就是常用的数组，只是换了个名字而已。 例如使用顺序表存储 {1,3,5,7,9}，如图所示：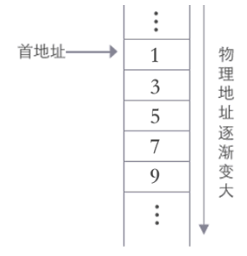 
由于顺序表结构的底层实现借助的就是数组，因此对于初学者来说，可以把顺序表完全等价为数组，但实则不是这样。数据结构是研究数据存储方式的一门学科，它囊括的都是各种存储结构，而数组只是各种编程语言中的基本数据类型，并不属于数据结构的范畴。
链表(linked list)
对于使用顺序表(底层实现靠数组)时，需要提前申请一定大小的存储空间，这块存储空间的物理地址是连续的，链表则完全不同，使用链表存储数据时，是随用随申请，因此数据的存储位置是相互分离的，换句话说，数据的存储位置是随机的。
为了给各个数据块建立 “依次排列(线性表特性)” 的关系，链表给各数据块增设一个指针，每个数据块的指针都指向下一个数据块（最后一个数据块的指针指向 NULL）。就如同一个个小学生都伸手去拉住下一个小学生的手，这样，看似毫无关系的数据块就建立了“依次排列”的关系，也就形成了链表，如图所示：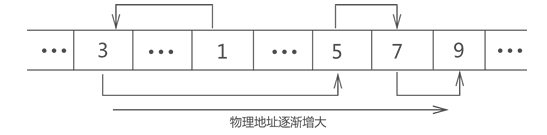 
栈和队列(Stack and queue)
栈和队列隶属于线性表，是特殊的线性表，因为它们对线性表中元素的进出做了明确的要求。 栈中的元素只能从线性表的一端进出（另一端封死），且要遵循“先入后出”的原则，即先进栈的元素后出栈。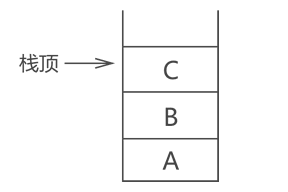 
解释：栈结构如上图所示，像一个木桶，栈中含有 3 个元素，分别是 A、B 和 C，从在栈中的状态可以看出 A 最先进的栈，然后 B 进栈，最后 C 进栈。根据“先进后出”的原则，3 个元素出栈的顺序应该是：C 最先出栈，然后 B 出栈，最后才是 A 出栈。
队列中的元素只能从线性表的一端进，从另一端出，且要遵循“先入先出”的特点，即先进队列的元素也要先出队列。 
解释：队列结构如上图所示，队列中有 3 个元素，分别是 A、B 和 C，从在队列中的状态可以看出是 A 先进队列，然后 B 进，最后 C 进。根据“先进先出”的原则，3 个元素出队列的顺序应该是 A 最先出队列，然后 B 出，最后 C 出。
树存储结构适合存储具有“一对多”关系的数据，就像一棵树有多个树枝。 
如图所示，其中张平只有一个父亲，但他却有两（多）个孩子，这就是“一对多”的关系，满足这种关系的数据可以使用树存储结构。
图存储结构适合存储具有“多对多”关系的数据。 
如图所示，从 V1 可以到达 V2、V3、V4，同样，从 V2、V3、V4 也可以到达 V1，同理V3与V4。这就是“多对多”的关系，满足这种关系的数据可以使用图存储结构。
