剪邮票
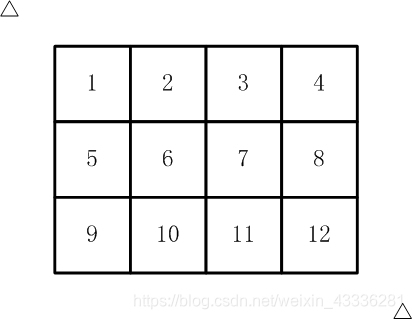如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
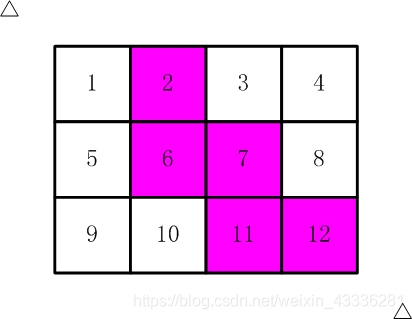
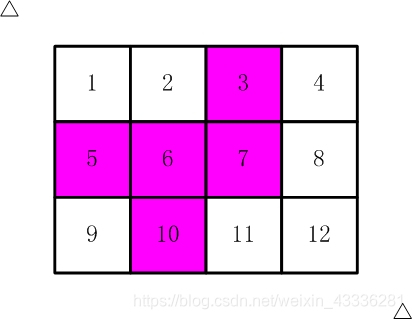
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。
请你计算，一共有多少种不同的剪取方法。
请填写表示方案数目的整数。 注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。
Ideas最终是想让我们计算”一共有多少种不同的剪取方法“，所以是要搜索所有的状态空间，应该用DFS。
这道题其实就是从12个格子中选出来5个，保证5个格子是联通的。
所以我们可以把问题建模：一个长度为12、元素为0的列表，从中选择5个格子置为1，然后判断5个1的位置对应到矩阵上是不是连通的。
我觉得这道题的考点就是连通块检查，连通块检查可以定义为一个单独的函数，经典的连通块计算方法还是通过DFS。
对于一个矩阵，首先要定义一个变量cnt，用于统计矩阵中为1的元素个数，然后整个遍历一遍矩阵，找到第一个为1的位置，先把 cnt + 1，然后进行 DFS，从当前位置开始，四个方向扩散，如果遇到值为1的元素，则置为0。
注意哈，此时如果所有的1是连通的，那么我从一个1出发，就可以将所有的1都置为0，后面继续遍历矩阵就不会再遇到值为1的元素，所以最后判断是不是连通块就是判断 cnt == 1。
OK，然后就可以开始写代码啦。
Code C++#include #include using namespace std; int ans; bool check(int arr[12]); void dfs(int g[3][4], int i, int j); int main(int argc, const char *argv[]) { int per[] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1}; do { if (check(per)) ans++; } while (next_permutation(per, per + 12)); cout << ans << endl; return 0; } bool check(int arr[12]) { int g[3][4]; memset(g, 0, sizeof(g)); //将相应位置标注为1 for (int i = 0; i < 3; ++i) { for (int j = 0; j < 4; ++j) { if (arr[i * 4 + j] == 1)g[i][j] = 1; } } // 经典连通块计算 int cnt = 0; for (int i = 0; i < 3; ++i) { for (int j = 0; j < 4; ++j) { if (g[i][j] == 1) { dfs(g, i, j); cnt++; } } } return cnt == 1; } void dfs(int g[3][4], int i, int j) { g[i][j] = 0; if (i + 1 <= 2 && g[i + 1][j] == 1) dfs(g, i + 1, j); if (i - 1 >= 0 && g[i - 1][j] == 1) dfs(g, i - 1, j); if (j + 1 <= 3 && g[i][j + 1] == 1) dfs(g, i, j + 1); if (j - 1 >= 0 && g[i][j - 1] == 1) dfs(g, i, j - 1); }
Python
from copy import deepcopy from itertools import permutations def check(m): def dfs(x, y): m[x][y] = 0 for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]: nx, ny = x + dx, y + dy if -1 < nx < len(m) and -1 < ny < len(m[0]) and m[nx][ny] == 1: dfs(nx, ny) cnt = 0 for r in range(3): for c in range(4): if m[r][c] == 1: dfs(r, c) cnt += 1 return cnt == 1 if __name__ == '__main__': ans = set() state = [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1] matrix = [[0] * 4 for _ in range(3)] for ste in permutations(state): # 将一维状态向量映射为二维矩阵 for i in range(3): for j in range(4): matrix[i][j] = ste[i * 4 + j] string = ''.join([''.join(map(str, row)) for row in matrix]) if check(deepcopy(matrix)) and string not in ans: # 连通块检查 print(string) ans.add(string) print(len(ans))Answer: 116
